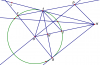
Cho đường tròn(O;R) và một cát tuyến d ko đi qua tâm đường tròn . Từ một điểm M trên d và ở ngoài đường tròn vẽ 2 tiếp tuyến MA, MB. Đường thẳng BO cắt đường tròn tại C . Từ O vẽ đường thẳng vuông góc với BC cắt CA ở D
A. Ch/m MD=OC
B. Xác định điểm M trên d để tam giác MAB đều
C. OM cắt AB tại H và đường tròn (O) tại I .ch/m IM.AH= IH.AM
____________________________________________________
a) Dễ dàng chứng minh được: $OBMA$ nội tiếp
Ta có: [tex]\widehat{CAx}=\widehat{CBA}[/tex] (Cùng chắn cung $AC$)
[tex]\widehat{CBA}=\widehat{OMA}(OBMAnt)[/tex]
Mà: [tex]\widehat{CAx}=\widehat{DAM}(d^2)[/tex]
[tex]\Rightarrow \widehat{DAM}=\widehat{OMA}\Rightarrow AD\parallel OM(1)[/tex]
Ta lại có: [tex]\widehat{BCA}=\widehat{ABM}[/tex]
Mà: [tex]\widehat{ABM}=\widehat{AOM}[/tex]
[tex]\Rightarrow \widehat{BCA}=\widehat{AOM}[/tex]
Xét: [tex]\Delta COD[/tex] và [tex]\Delta OAM[/tex] có:
[tex]OC=OA(=R)[/tex]
[tex]\widehat{COD}=\widehat{OAM}(=90^{\circ})[/tex]
[tex]\widehat{OCD}=\widehat{AOM}(cmt)[/tex]
[tex]\Rightarrow \Delta COD= \Delta OAM(g.c.g)[/tex]
$ \Rightarrow CD=OM$ (2)
Từ $(1)'(2)$ suy ra: [tex]OCDM[/tex] là hình bình hành
Nên: $CO=DM$
b) [tex]\Delta AMB[/tex] đều
[tex]\Leftrightarrow \widehat{AMB}=60^{\circ}\Leftrightarrow \widehat{AMO}=30^{\circ}\Leftrightarrow OA=\frac{1}{2}OM\Leftrightarrow OM=2R[/tex]
Vậy khi [tex]M\in (d)[/tex] sao cho $OM=2R$ thì..
c) Ta có: [tex]\widehat{IAB}=\frac{1}{2}\widehat{BOI};\widehat{IAM}=\frac{1}{2}\widehat{AOI}[/tex]
Mà: $\widehat{BOI}=\widehat{AOI} $
[tex]\Rightarrow \widehat{IAB}=\widehat{IAM}[/tex]
[tex]\Rightarrow AI[/tex] là phân giác góc $HAM$
[tex]\Rightarrow \frac{AH}{AM}=\frac{HI}{IM}\Rightarrow AH.MI=HI.AM[/tex] ($dpcm$)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
