[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Thời gian đi từ [imath]x_1\to x_2[/imath]
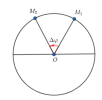
I.1 Thời gian ngắn nhất vật đi từ [imath]x_1[/imath] đến [imath]VTCB[/imath] và đến vị trí biên.
Các dạng toán: Thời gian + thời điểm.
Phương pháp chung:
Cách 1: Dùng [imath]VTLG: \begin{cases} \text{xác định góc quét tương ứng với sự dịch chuyển} \ \Delta \varphi \\ \text{Thời gian}: t=\dfrac{\Delta \varphi}{\omega}\end{cases}[/imath]
(* với những góc hay vị trí đặc biệt có thể dùng trục thời gian.)
Cách 2: Dùng phương trình lượng giác: [imath]\begin{cases} x_1=A\sin\omega t_1\Rightarrow \sin \omega t_1=\dfrac{x_1}{A} \Rightarrow t_1=\dfrac{1}{\omega}\arcsin\dfrac{x_1}{A}\\ x_1=A\cos\omega t_2\Rightarrow \cos \omega t_2=\dfrac{x_2}{A} \Rightarrow t_2=\dfrac{1}{\omega}\arccos\dfrac{x_2}{A}\end{cases}[/imath]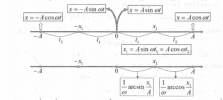
Ví dụ: Một chất điểm dao động điều hòa với biên độ [imath]6cm[/imath] và tần số góc [imath]10(rad/s)[/imath]. Khoảng thời gian ngắn nhất để nó đi từ li độ [imath]3cm[/imath] đến [imath]VTCB[/imath] là:
Cách 1: Dùng [imath]VTLG[/imath]
| Ta có thời gian ngắn nhất là: [imath]t=\dfrac{\Delta \varphi}{\omega}=\dfrac{\dfrac{\pi}{6}}{10}=\dfrac{\pi}{60}(s)[/imath] * Có thể dùng trục thời gian: Thời gian ngắn nhất đi từ vị trí [imath]\dfrac{A}{2}\to[/imath] [imath]VTCB[/imath] chính bằng [imath]\dfrac{T}{12}=\dfrac{\pi}{60}(s)[/imath] |  |
Cách 2: Dùng phương trình lượng giác:
[imath]t_1=\dfrac{1}{\omega}\arcsin\dfrac{x_1}{A}=\dfrac{1}{10}\arcsin\dfrac{3}{6}=\dfrac{\pi}{60}(s)[/imath]
Nhận xét: Thoạt nhìn có vẻ phương pháp hai tối ưu thời gian và ngắn gọn hơn, nhưng thật ra phương pháp này chỉ tốt cho những bài toán vật không đi quá một chu kì, để mở rộng bài toán cần thành thục phương pháp đầu tiên đồng thời học thuộc trục thời gian để tiết kiệm thời gian tính toán.
I.2 Thời gian ngắn nhất đi từ [imath]x_1[/imath] đến [imath]x_2[/imath]
Về mặt phương pháp giống giạng trên vì vậy ta rút ra phương pháp giải bài này như sau:
+ Vật chuyển động trong nhiều chu kì, sử dụng vòng tròn lượng giác xác định góc quét và rút ra thời gian: [imath]t=\dfrac{\Delta \varphi}{\omega}[/imath]
Ví dụ: Một vật dao động điều hòa có phương trình li độ [imath]x=10cos(5t)[/imath]. Thời gian ngắn nhất vật đi từ li độ [imath]7cm[/imath] đên li độ [imath]2cm[/imath] là:
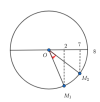
Áp dụng công thức: [imath]\Delta t=\dfrac{|\arccos \dfrac{x_2}{A}-\arccos \dfrac{x_1}{A}|}{\omega}=\dfrac{|\arccos \dfrac{2}{10}-\arccos \dfrac{7}{10}|}{5}=0,114(s)[/imath]
Bài tập luyện tập:
Câu 1: Vật dao động điều hòa với biên độ [imath]A[/imath], thời gian ngắn nhất vật đi từ li độ [imath]x=+A[/imath] đến li độ [imath]x=\dfrac{A}{3}[/imath] là [imath]0,1s[/imath]. Chu kì dao động của vật là:[imath]A.1,85s \quad B.1,2s \quad C.0,51s \quad D.0,4s[/imath]
Câu 2: Vật dao động điều hòa với biên độ [imath]A[/imath] với chu kì [imath]T[/imath], thời gian ngắn nhất vật đi từ li độ [imath]x+=A[/imath] tới li độ [imath]x=\dfrac{A}{5}[/imath] là [imath]T-0,45[/imath] s. Giá trị [imath]T[/imath] gần nhất với:
[imath]A.0,57s \quad B.1,2s \quad C.0,51s \quad D.0,4s[/imath]
Câu 3: Một chất điểm dao động điều hòa với chu kì [imath]1s[/imath] với biên độ [imath]4,5cm[/imath]. Khoảng thời gian trong một chu kì để vật cách vị trí cân bằng một khoảng nhỏ hơn [imath]2cm[/imath] là:
[imath]A.0,29s \quad B.16,80s \quad C.0,71s \quad D.0,15s[/imath]
Câu 4: Một dao động điều hòa có chu kì dao động là [imath]T[/imath] và biên độ là [imath]A[/imath]. Tại thời điểm ban đầu vật có ly độ là [imath]x_1>0[/imath]. Thời gian ngắn nhất để vật đi từ vị trí ban đầu về vị trí cân bằng gấp ba thời gian ngắn nhất để vật đi từ vị trí ban đầu đến vị trí biên [imath]x+=A[/imath]. Chọn phương án đúng.
[imath]A.x_1=0,924A \quad B.x_1=0,5A\sqrt{3} \quad C.0,5A\sqrt{2} \quad D.0,021A[/imath]
Câu 5: Một vật dao động điều hoà có phương trình li độ [imath]x=8 \cos (7 \pi t+\pi / 6) cm[/imath]. Khoảng thời gian tối thiểu để vật đi từ li độ [imath]4 \sqrt{2} cm[/imath] đến li độ [imath]-4 \sqrt{3} cm[/imath] là
[imath]A. 1 / 24 s \quad B. 5 / 12 s \quad C. 1 / 6 s\quad D. 1 / 12 s[/imath].
Câu 6: Một con lắc lò xo đang dao động điêu hòa với biên độ [imath]A[/imath], thời gian ngắn nhất để con lắc di chuyển từ vị trí có li độ [imath]x_1=-A[/imath] đến vị trí có li độ [imath]x_2=A / 2[/imath] là [imath]1s[/imath] . Chu kì dao động của con lắc là:
[imath]A. 6s\quad B.1 / 3s \quad C. 2 s\quad D. 3 s\quad[/imath]
Câu 7: Một vật dao động với phương trình [imath]x=6 \cos (4 \pi t+\pi / 6)[/imath] ([imath]t[/imath] tính bằng [imath]s[/imath]). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ [imath]3cm[/imath] theo chiều dương đến vị trí có li độ [imath]-3 \sqrt{3} cm[/imath] là:
[imath]A. 7 / 24 s\quad B. 1 / 4s\quad C. 5 / 24 s \quad D. 1 / 8 s[/imath]
Bạn đọc tham khảo thêm
Tổng hợp tất tần tật về dao động điều hòa
Attachments
Last edited:
