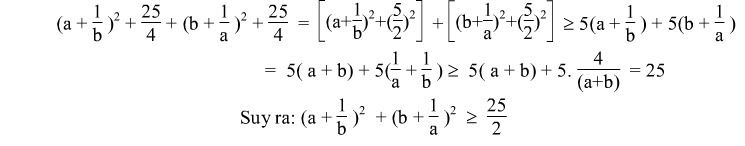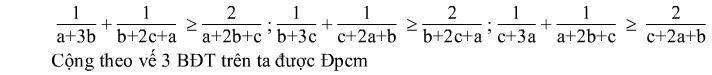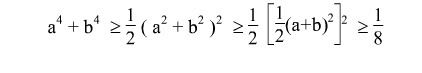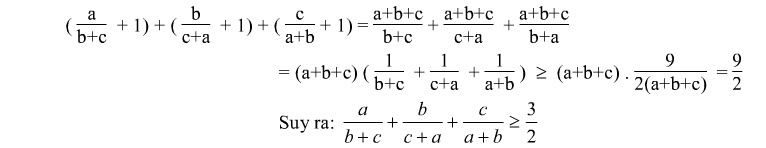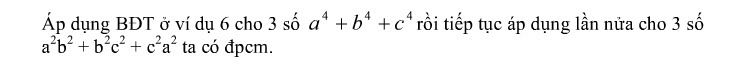Chuyên đề bất đẳng thức Cô sin & buhiacôpski

[trang4t]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Câu 1: Cho 2 số dương a.b có tổng bằng 1. CMR
( a + 1/b )^2 + ( b+ 1/a )^2 \geq 25/2

Câu 2: CM BĐT sau với mọi a,b,c > 0
1/a+3b + 1/b+3c + 1/c+3a \geq 1/a+2b+c + 1/b+2c+a + 1/c+2a+b

Câu 3: Cho a,b,c là 3 số dương:
Chứng minh: a/bc + b/ac + c/ab \geq 1/a + 1/b + 1/c

Câu 4: Chứng minh a^4 + b^4 \geq 1/8 với a + b \geq 1

Câu 5: Chứng minh a/b+c + b/c+a + c/a+b \geq 3/2 Với a,b,c > 0

Câu 6: Chứng minh a^4 + b^4 + c^4 \geq abc (a + b + c)

Câu 7: Cho a,b,c là các số thực và a+ b+ c = 1
CMR a^2 + b^2 + c^2 \geq 1/3

* Cố gắng júp mình nké các b ơi. t tk nhìu :khi (86):

 

[tuananh8]

Câu 2: CM BĐT sau với mọi a,b,c > 0
1/a+3b + 1/b+3c + 1/c+3a \geq 1/a+2b+c + 1/b+2c+a + 1/c+2a+b

Ta có:

[TEX]\frac{1}{a+3b}+\frac{1}{b+2c+a} \geq \frac{4}{2a+4b+2c}=\frac{2}{a+2b+c}[/TEX]

Tương tự:

[TEX]\frac{1}{b+3c}+\frac{1}{c+2a+b} \geq \frac{2}{a+b+2c}[/TEX]

[TEX]\frac{1}{c+3a}+\frac{1}{a+2b+c} \geq \frac{2}{2a+b+c}[/TEX]

Cộng 3 vế 3 BĐT trên có đpcm.

 

[vnzoomvodoi]

Câu 1: Sorry mình nhìn nhầm số!
Áp dụng bđt B ta được bt đã cho >=(a+b+1/a+1/b)^2/2 >=(1+4(a+b))^2/2=25/2
Dấu = xảy ra a=b=1/2

Câu 7: Áp dụng trực tiếp bđt Bunyakovski cho 3 số.
Câu 6: [tex]a^2bc/geq/a^2((b^2+c^2)/2)[/tex]
Lại Cô-si một lần nữa dưới dạng [tex]a^2+b^2+c^2\geq\ab+bc+ab[/tex] ra đpcm
Câu 5: Áp dụng bđt Schwarz
Câu 4: [tex]a^4+b^4\geq\frac{(a^2+b^2)^2}{2}\geq\frac{(a+b)^2/2}{2}\geq1/8[/tex]
Câu 3: Qui đồng lên rồi áp dụng bđt

 

[minhnam138]

Câu 6:
SD liên tục[TEX]x^2 + y^2 +z^2 \geq xy + yz + xz[/TEX] ta dc
[TEX]a^4 + b^4 + c^4 \geq a^2b^2 + b^2c^2 + c^2a^2 \geq ab^2c + a^2bc + abc^2 = abc(a+ b + c)[/TEX]

 

[duynhan1]

Câu 3 Cô si từng cặp cộng lại có điều phải chứng minh

 

[albee_yu]

Câu 1:

Câu 2:

Câu 3:

Câu 4:

Câu 5:

Câu 6:

Câu 7: