[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các bạn, ở bài viết này mình sẽ tổng hợp kiến thức cơ bản liên quan đến chương này nhé. 
I. Đơn vị đo góc và cung tròn
- Khái niệm về radian: Cung có độ dài bằng bán kính đường tròn chắn cung đó thì có số đo là 1 radian, kí hiệu [imath]1 rad[/imath] hoặc có thể bỏ [imath]rad[/imath].
- Quan hệ giữa radian và độ: [imath]180^o=\pi rad \Rightarrow 1^o=\dfrac{\pi}{180} rad, 1 rad =\dfrac{180}{\pi} ^o[/imath]
- Độ dài cung radian: Một cung của đường tròn bán kính [imath]r[/imath] và có số đo là [imath]\alpha rad[/imath] thì có độ dài [imath]l=R \alpha[/imath]
II. Góc và cung lượng giác
- Khái niệm đường tròn định hướng: Đường tròn định hướng là đường tròn có chiều di động được quy ước: chiều dương là chiều ngược hướng đồng hồ, chiều âm là chiều kim đồng hồ.
- Các khái niệm trên đường tròn định hướng:
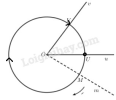
+ Góc lượng giác: Khi tia [imath]Om[/imath] quay theo cùng 1 chiều từ tia [imath]Ou[/imath] đến tia [imath]Ov[/imath] thì nó quét 1 góc lượng giác với tia đầu là [imath]Ou[/imath], tia cuối là [imath]Ov[/imath], kí hiệu [imath](Ou,Ov)[/imath]
+ Cung lượng giác: Khi tia [imath]Om[/imath] quét theo 1 góc lượng giác [imath](Ou,Ov)[/imath] thì điểm M chạy trên 1 đường tròn theo 1 chiều từ U tới V. Khi đó điểm M vạch nên 1 cung lượng giác có điểm đầu là U điểm cuối là V tương ứng với góc lượng giác.
- Nếu 1 góc lượng giác có số đo [imath]\alpha (rad)[/imath] thì mọi góc lượng giác có cùng tia đầu và tia cuối đều có số đo dạng [imath]\alpha +2k\pi (rad)[/imath] [imath](k \in \mathbb{Z})[/imath]
- Nếu 1 cung lượng giác có số đo [imath]\alpha (rad)[/imath] thì mọi cung lượng giác có cùng tia đầu và tia cuối đều có số đo dạng [imath]\alpha +2k\pi (rad)[/imath] [imath](k \in \mathbb{Z})[/imath]
- Hệ thức Chasles(Sa-lơ): [imath](OA,OC)+(OC,OB)=(OA,OB)+2k\pi[/imath]
III. Biểu diễn cung lượng giác trên đường tròn lượng giác
- Đường tròn lượng giác là đường tròn định hướng có bán kính là 1 và tâm là gốc hệ trục tọa độ. Điểm gốc của cung lượng giác là [imath]A(1,0)[/imath].
- Biểu diễn cung lượng giác [imath]\alpha[/imath] trên đường tròn lượng giác là chọn điểm M trên đường tròn lượng giác sao cho số đo cung [imath]AM[/imath] bằng [imath]\alpha[/imath].
IV. Một số công thức lượng giác
- Các công thức cộng, trừ góc:
+ [imath]\cos (a \pm b) =\cos a \cos b \mp \sin a \sin b[/imath]
+ [imath]\sin (a \pm b) = \sin a \cos b \pm \sin b \cos a[/imath]
+ [imath]\tan (a \pm b) = \dfrac{\tan a \pm \tan b}{1 \mp \tan a \tan b}[/imath]
- Công thức nhân đôi góc:
+ [imath]\cos 2x=\cos ^2x-\sin^2x=2\cos^2x-1=1-2\sin^2x[/imath]
+ [imath]\sin 2x=2\sin x\cos x[/imath]
+ [imath]\tan 2x=\dfrac{2\tan x}{1-\tan^2x}[/imath]
- Công thức hạ bậc:
+ [imath]\cos ^2x=\dfrac{1+\cos 2x}{2}[/imath]
+ [imath]\sin ^2x=\dfrac{1-\cos 2x}{2}[/imath]
- Công thức nhân 3 góc:
+ [imath]\sin 3x=3\sin x-4\sin ^3x[/imath]
+ [imath]\cos 3x=4\cos^3x-3\cos x[/imath]
+ [imath]\tan 3x=\dfrac{\tan ^3x-3\tan x}{3\tan^2x-1}[/imath]
- Công thức biến đổi tích thành tổng:
+ [imath]\cos x \cos y=\dfrac{1}{2}[\cos (x-y)+\cos (x+y)][/imath]
+ [imath]\sin x \sin y =\dfrac{1}{2}[\cos (x-y)-\cos (x+y)][/imath]
+ [imath]\sin x \cos y=\dfrac{1}{2}[\sin (x+y)+\sin (x-y)][/imath]
- Công thức biến đổi tổng thành tích:
+ [imath]\sin x+\sin y=2\sin \dfrac{x+y}{2} \cos \dfrac{x-y}{2}[/imath]
+ [imath]\cos x+\cos y=2\cos \dfrac{x+y}{2} \cos \dfrac{x-y}{2}[/imath]
+ [imath]\sin x+\cos x=\sin (x+\dfrac{\pi}{4})[/imath]
+ [imath]\sin x-\cos x=\sin (x-\dfrac{\pi}{4})[/imath]
I. Đơn vị đo góc và cung tròn
- Khái niệm về radian: Cung có độ dài bằng bán kính đường tròn chắn cung đó thì có số đo là 1 radian, kí hiệu [imath]1 rad[/imath] hoặc có thể bỏ [imath]rad[/imath].
- Quan hệ giữa radian và độ: [imath]180^o=\pi rad \Rightarrow 1^o=\dfrac{\pi}{180} rad, 1 rad =\dfrac{180}{\pi} ^o[/imath]
- Độ dài cung radian: Một cung của đường tròn bán kính [imath]r[/imath] và có số đo là [imath]\alpha rad[/imath] thì có độ dài [imath]l=R \alpha[/imath]
II. Góc và cung lượng giác
- Khái niệm đường tròn định hướng: Đường tròn định hướng là đường tròn có chiều di động được quy ước: chiều dương là chiều ngược hướng đồng hồ, chiều âm là chiều kim đồng hồ.
- Các khái niệm trên đường tròn định hướng:
+ Góc lượng giác: Khi tia [imath]Om[/imath] quay theo cùng 1 chiều từ tia [imath]Ou[/imath] đến tia [imath]Ov[/imath] thì nó quét 1 góc lượng giác với tia đầu là [imath]Ou[/imath], tia cuối là [imath]Ov[/imath], kí hiệu [imath](Ou,Ov)[/imath]
+ Cung lượng giác: Khi tia [imath]Om[/imath] quét theo 1 góc lượng giác [imath](Ou,Ov)[/imath] thì điểm M chạy trên 1 đường tròn theo 1 chiều từ U tới V. Khi đó điểm M vạch nên 1 cung lượng giác có điểm đầu là U điểm cuối là V tương ứng với góc lượng giác.
- Nếu 1 góc lượng giác có số đo [imath]\alpha (rad)[/imath] thì mọi góc lượng giác có cùng tia đầu và tia cuối đều có số đo dạng [imath]\alpha +2k\pi (rad)[/imath] [imath](k \in \mathbb{Z})[/imath]
- Nếu 1 cung lượng giác có số đo [imath]\alpha (rad)[/imath] thì mọi cung lượng giác có cùng tia đầu và tia cuối đều có số đo dạng [imath]\alpha +2k\pi (rad)[/imath] [imath](k \in \mathbb{Z})[/imath]
- Hệ thức Chasles(Sa-lơ): [imath](OA,OC)+(OC,OB)=(OA,OB)+2k\pi[/imath]
III. Biểu diễn cung lượng giác trên đường tròn lượng giác
- Đường tròn lượng giác là đường tròn định hướng có bán kính là 1 và tâm là gốc hệ trục tọa độ. Điểm gốc của cung lượng giác là [imath]A(1,0)[/imath].
- Biểu diễn cung lượng giác [imath]\alpha[/imath] trên đường tròn lượng giác là chọn điểm M trên đường tròn lượng giác sao cho số đo cung [imath]AM[/imath] bằng [imath]\alpha[/imath].
IV. Một số công thức lượng giác
- Các công thức cộng, trừ góc:
+ [imath]\cos (a \pm b) =\cos a \cos b \mp \sin a \sin b[/imath]
+ [imath]\sin (a \pm b) = \sin a \cos b \pm \sin b \cos a[/imath]
+ [imath]\tan (a \pm b) = \dfrac{\tan a \pm \tan b}{1 \mp \tan a \tan b}[/imath]
- Công thức nhân đôi góc:
+ [imath]\cos 2x=\cos ^2x-\sin^2x=2\cos^2x-1=1-2\sin^2x[/imath]
+ [imath]\sin 2x=2\sin x\cos x[/imath]
+ [imath]\tan 2x=\dfrac{2\tan x}{1-\tan^2x}[/imath]
- Công thức hạ bậc:
+ [imath]\cos ^2x=\dfrac{1+\cos 2x}{2}[/imath]
+ [imath]\sin ^2x=\dfrac{1-\cos 2x}{2}[/imath]
- Công thức nhân 3 góc:
+ [imath]\sin 3x=3\sin x-4\sin ^3x[/imath]
+ [imath]\cos 3x=4\cos^3x-3\cos x[/imath]
+ [imath]\tan 3x=\dfrac{\tan ^3x-3\tan x}{3\tan^2x-1}[/imath]
- Công thức biến đổi tích thành tổng:
+ [imath]\cos x \cos y=\dfrac{1}{2}[\cos (x-y)+\cos (x+y)][/imath]
+ [imath]\sin x \sin y =\dfrac{1}{2}[\cos (x-y)-\cos (x+y)][/imath]
+ [imath]\sin x \cos y=\dfrac{1}{2}[\sin (x+y)+\sin (x-y)][/imath]
- Công thức biến đổi tổng thành tích:
+ [imath]\sin x+\sin y=2\sin \dfrac{x+y}{2} \cos \dfrac{x-y}{2}[/imath]
+ [imath]\cos x+\cos y=2\cos \dfrac{x+y}{2} \cos \dfrac{x-y}{2}[/imath]
+ [imath]\sin x+\cos x=\sin (x+\dfrac{\pi}{4})[/imath]
+ [imath]\sin x-\cos x=\sin (x-\dfrac{\pi}{4})[/imath]
Last edited:
