[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
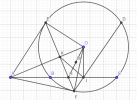
Cho 3 điểm [imath]\mathrm{A} ; \mathrm{B} ; \mathrm{C}[/imath] cố định thẳng hàng theo thứ tự đó. Vẽ đường trò̀n [imath](\mathrm{O})[/imath] bá qua [imath]\mathrm{B}[/imath] và [imath]\mathrm{C}(\mathrm{BC}[/imath] khác đường kính). Từ [imath]\mathrm{A}[/imath] kẻ các tiếp tuyến [imath]\mathrm{AE}[/imath] và [imath]\mathrm{AF}[/imath] đến [imath](\mathrm{O})(\mathrm{E} ; \mathrm{F}[/imath] tiếp điểm). Gọi I là trung điềm của [imath]\mathrm{BC}[/imath]; giao điểm của [imath]\mathrm{FI}[/imath] với [imath](\mathrm{O})[/imath] là [imath]\mathrm{D}[/imath].
1. Chứng minh các tứ giác [imath]\mathrm{AEOF}[/imath] và [imath]\mathrm{AEOI}[/imath] nội tiếp.
2. Chứng minh [imath]\mathrm{AE}^{2}=\mathrm{AB} \cdot \mathrm{AC}[/imath] và [imath]\mathrm{ED}[/imath] song song với [imath]\mathrm{AC}[/imath].
3. Khi [imath](\mathrm{O})[/imath] thay đồi nhưng vẫn đi qua [imath]\mathrm{B}[/imath] và [imath]\mathrm{C}[/imath], gọi [imath]\mathrm{K}[/imath] là trung điểm [imath]\mathrm{EF}[/imath] hãy chứng tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc một đường thằng cố định.
giúp em mình câu 3 thôi ạ
@Cáp Ngọc Bảo Phương @chi254 @Mộc Nhãn @HT2k02(Re-kido)
1. Chứng minh các tứ giác [imath]\mathrm{AEOF}[/imath] và [imath]\mathrm{AEOI}[/imath] nội tiếp.
2. Chứng minh [imath]\mathrm{AE}^{2}=\mathrm{AB} \cdot \mathrm{AC}[/imath] và [imath]\mathrm{ED}[/imath] song song với [imath]\mathrm{AC}[/imath].
3. Khi [imath](\mathrm{O})[/imath] thay đồi nhưng vẫn đi qua [imath]\mathrm{B}[/imath] và [imath]\mathrm{C}[/imath], gọi [imath]\mathrm{K}[/imath] là trung điểm [imath]\mathrm{EF}[/imath] hãy chứng tâm đường tròn ngoại tiếp tam giác OIK luôn thuộc một đường thằng cố định.
giúp em mình câu 3 thôi ạ
@Cáp Ngọc Bảo Phương @chi254 @Mộc Nhãn @HT2k02(Re-kido)
Attachments
Last edited by a moderator: