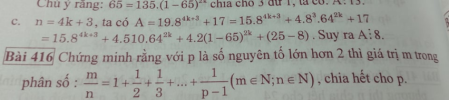Nguyễn Chi XuyênTa có: [imath]\dfrac{m}{n} = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{p-1}[/imath]
[imath]= \dfrac{p}{1 (p-1)} + \dfrac{p}{2(p-2)} + \cdots[/imath]
[imath]= \dfrac{p.A}{(p-1)!}[/imath] (chỗ này A là 1 biểu thức nào đó của quy đồng, mình chỉ quan tâm có p ở tử là được)
Dễ thấy vì p là số nguyên tố nên [imath](p-1)![/imath] không chia hết cho p nên m sẽ chia hết cho p.
(Đơn giản chỗ này mình nghĩ kiểu, với mọi cách rút gọn phân số ở Vế phải á, thì tử số luôn luôn có p, nên tử số vế trái cũng luôn chứa nhân tử p. nghĩa là nó phải chia hết cho p).
Bài toán được chứng minh!.
-Ngoài ra , mời e tham khảo thêm các bài toán số học tại: [Lý thuyết] Chuyên đề HSG: Số học
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
