[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
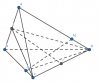
Cho tứ diện $ABCD$. Gọi $I,J$ lần lượt là trung điểm các cạnh $AB,CD$
a) Chứng minh $\overrightarrow{BC},\overrightarrow{IJ},\overrightarrow{AD}$ đồng phẳng
b) Lấy hai điểm $M,N$ thoả mãn $\overrightarrow{AM}=3\overrightarrow{MD}$ và $\overrightarrow{BN}=3\overrightarrow{NC}$. Chứng minh $\overrightarrow{MN},\overrightarrow{AB},\overrightarrow{DC}$ đồng phẳng
Em còn 2 bài toán hình chưa làm được .Mọi người giúp em 2 bài nhé
a) Chứng minh $\overrightarrow{BC},\overrightarrow{IJ},\overrightarrow{AD}$ đồng phẳng
b) Lấy hai điểm $M,N$ thoả mãn $\overrightarrow{AM}=3\overrightarrow{MD}$ và $\overrightarrow{BN}=3\overrightarrow{NC}$. Chứng minh $\overrightarrow{MN},\overrightarrow{AB},\overrightarrow{DC}$ đồng phẳng
Em còn 2 bài toán hình chưa làm được .Mọi người giúp em 2 bài nhé
Attachments
Last edited by a moderator: