Giúp mình câu 6, 7 với ạ.
View attachment 182242
Tui góp 1 câu :>
Câu 6:
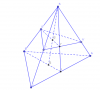
Gọi $I$ là trung điểm $AC=> SI \subset (SBG)$
Trong $\Delta CSA$; gọi $I'=SI \cap A'C'$
$=> B'I'=(SBI) \cap (A'B'C')$
Mà $SG \subset (SBI)=> SG \cap (A'B'C')=SG \cap BI'=G'$
(trông lủng lủng sao á).
Xét $\Delta SAC$ với $I$ là trung điểm cạnh $AC$; $C' \in SC$ và $A; \in SA;I'=A'C'=SI$
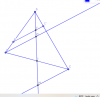
Từ $A$ và $C$ lần lượt kẻ các đường thẳng song song với $A'C'$; cắt $SI$ lần lượt tại $D$ và $H$.
$=> \Delta ADI= \Delta CHI=> ID=IH$
Ta có: $\frac{SA}{SA'}=\frac{SD}{SI'}=\frac{SI-ID}{SI'}(1)$
$\frac{SC}{SC'}=\frac{SH}{SI'}=\frac{SI+IH}{SI'}(2)$
Từ $(1)$ và $(2)=> \frac{SA}{SA'}+\frac{SC}{SC'}=\frac{SI-ID}{SI'}+\frac{SI+IH}{SI'}=2.\frac{SI}{SI'}(*)$.
Xét $\Delta SBI$:
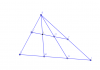
Gọi $M$ là trung điểm $BG$; $L=B'I' \cap SM$
Chứng minh tương tự như phần $\Delta SAC$:
$\frac{SB}{SB'}+\frac{SG}{SG'}=2.\frac{SM}{SL}(3)$
$4.\frac{SG}{SG'}=2.\frac{SM}{SL}+2.\frac{SI}{SI'}(4)$
Trừ theo từng về của $(4)$ cho $(3)$
$=> 3.\frac{SG}{SG'}=2.\frac{SI}{SI'}+\frac{SB}{SB'}(**)$
Từ $(*)$ và $(**)$ $=>\frac{SA}{SA'} +\frac{SB}{SB'}+\frac{SC}{SC'}=3.\frac{SG}{SG'}.$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
