Toán 9 Chứng minh

[NikolaTesla]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

1.

2
.
3. Cho 433 điểm phân biệt nằm trong hoặc nằm trên các cạnh của một tam giác đều có cạnh bằng 36cm. Chứng minh rằng có thể vẽ được một hình tròn có bán kính bằng căn 3 cm chứa ít nhất 5 điểm trong số các điểm đã cho.
@shorlochomevn@gmail.com giúp mình với

 

[Love You At First Sight]

1.
View attachment 134969
2
.View attachment 134970
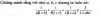
3. Cho 433 điểm phân biệt nằm trong hoặc nằm trên các cạnh của một tam giác đều có cạnh bằng 36cm. Chứng minh rằng có thể vẽ được một hình tròn có bán kính bằng căn 3 cm chứa ít nhất 5 điểm trong số các điểm đã cho.
@shorlochomevn@gmail.com giúp mình với

2.

 

[An Đăng Gia]

Câu 1:
Ta có: [tex]mn(mn+1)^{2}-(m+n)^{2}mn[/tex]
=[tex]mn(m^{2}n^{2}+2mn+1)-(m^{2}+2mn+n^{2})mn[/tex]
=[tex]mn(m^{2}n^{2}-m^{2}-n^{2}+1)[/tex]
=[tex]mn[m^{2}(n^{2}-1)-(n^{2}-1)][/tex]
=[tex][(m-1)m(m+1)][(n-1)n(n+1)][/tex]
Do (m-1)m(m+1) là tích 3 số nguyên liên tiếp (do m thuộc Z) nên sẽ có 1 số chia hết cho 2, 1 số chia hết cho 3 mà 2 và 3 nguyên tố cùng nhau nên (m-1)m(m+1) chia hết cho 6(1)
Tương tự ta chứng minh được (n-1)n(n+1) chia hết cho 6(2)
Từ (1) và (2) suy ra (m-1)m(m+1)(n-1)n(n+1) chia hết cho 36
Vậy [tex]mn(mn+1)^{2}-(m+n)^{2}mn[/tex] chia hết cho 36