- 5 Tháng hai 2020
- 2,742
- 4,788
- 531
- Hà Nội
- THCS Quang Minh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
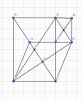
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H.
a) Tứ giác BCEQ là hình gì? Vì sao?
b) QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O.
Chứng minh rằng tam giác OEM là tam giác cân.
c) Chứng minh rằng ADEC là hình thang cân
d) Chứng minh rằng 3 điểm N, M, H thẳng hàng
Mn xem em làm câu c , d đúng chưa ạ
Em cảm ơn ạ .
a) Tứ giác BCEQ là hình gì? Vì sao?
b) QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O.
Chứng minh rằng tam giác OEM là tam giác cân.
c) Chứng minh rằng ADEC là hình thang cân
d) Chứng minh rằng 3 điểm N, M, H thẳng hàng
Mn xem em làm câu c , d đúng chưa ạ
Vì $BCEQ$ là hình thoi nên dễ dàng suy ra : $\begin{cases} BC \parallel QE \\ BC = QE \end{cases} \Leftrightarrow \begin{cases} QE \parallel AD \\ QE = AD \end{cases}$
Suy ra $EDAQ$ là hình bình hành nên $\widehat{DAQ} = \widehat{DEQ}$
$EH$ vừa là đường cao , trung tuyến $\Rightarrow \triangle QEC$ là $\triangle$ cân . Nên $\widehat{EQC} = \widehat{ECQ}$
Mà $AC \parallel DE \Rightarrow \widehat{CQE} = \widehat{QED} \Rightarrow \widehat{CQE} = \widehat{DAC} \Rightarrow \widehat{DAC} = \widehat{ECA} \Rightarrow ADEC \text{ là hình thang cân }$
Suy ra $EDAQ$ là hình bình hành nên $\widehat{DAQ} = \widehat{DEQ}$
$EH$ vừa là đường cao , trung tuyến $\Rightarrow \triangle QEC$ là $\triangle$ cân . Nên $\widehat{EQC} = \widehat{ECQ}$
Mà $AC \parallel DE \Rightarrow \widehat{CQE} = \widehat{QED} \Rightarrow \widehat{CQE} = \widehat{DAC} \Rightarrow \widehat{DAC} = \widehat{ECA} \Rightarrow ADEC \text{ là hình thang cân }$
Ta có :
$\widehat{NMD} + \widehat{DNQ} + \widehat{QMH} = ( \widehat{NMD} + \widehat{QMH} ) +90^o =( \widehat{NMD} + \widehat{NME})
+90^o = 90^o + 90^o = 180^o \\ \Rightarrow \text{ N ; M ; H thẳng hàng }$
$\widehat{NMD} + \widehat{DNQ} + \widehat{QMH} = ( \widehat{NMD} + \widehat{QMH} ) +90^o =( \widehat{NMD} + \widehat{NME})
+90^o = 90^o + 90^o = 180^o \\ \Rightarrow \text{ N ; M ; H thẳng hàng }$