Toán 9 Chứng minh tứ giác nội tiếp

[Trâm Lê]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại D, E. Tia phân giác BAC cắt tia phân giác DOE tại M. Trên nửa mặt phẳng bờ DM có chứa điểm B vẽ tia Dx sao cho MDx = MBC. Tia Dx cắt BC tại N. Chứng minh tứ giác MNCE nội tiếp.

 

[Lena1315]

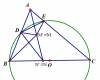
Gọi N' là giao điểm của đường phân giác góc BAC với BC.
Gọi M' là điểm thuộc AN sao cho [tex]\widehat{M'DN'} = \widehat{M'BN'}[/tex]
Suy ra tứ giác BDM'N' nội tiếp. [tex]\rightarrow \widehat{AM'D} = \widehat{ABC}[/tex]
Mà [tex]\widehat{ABC}=\widehat{AED}[/tex] (do tứ giác BDEC nội tiếp)
[tex]\rightarrow \widehat{AM'D}=\widehat{AED}[/tex]
[tex]\rightarrow[/tex] tứ giác ADM'E nội tiếp.
[tex]\rightarrow \widehat{ADE}=\widehat{AM'E}[/tex]
Mà [tex]\widehat{ADE}=\widehat{ACB}[/tex] (do tứ giác BDEC nội tiếp)
[tex]\rightarrow \widehat{AM'E}=\widehat{ACB} \Rightarrow \Delta{AM'E} \sim \Delta{ACN'}[/tex]
Suy ra [tex]\frac{M'E}{AM'} = \frac{N'C}{AC}[/tex] (1)
Từ [tex]\widehat{ABC} = \widehat{AM'D} \Rightarrow \Delta{ADM'} \sim \Delta{AN'B} \Rightarrow \frac{M'D}{AM'} = \frac{N'B}{AB}[/tex] (2)
Lại có AN' là phân giác góc BAC nên [tex]\frac{N'B}{N'C} = \frac{AB}{AC} \Rightarrow \frac{N'B}{AB} = \frac{N'C}{AC}[/tex] (3)
Từ (1,2,3) suy ra [tex]\frac{M'E}{AM'} = \frac{M'D}{AM'} \Rightarrow M'E = M'D[/tex]
Lại có OD=OE . Suy ra OM' là trung trực của DE. Suy ra OM' là phân giác của góc DOE.
Suy ra M' là giao 2 phân giác của 2 góc BAC và DOE nên [tex]M' \equiv M[/tex]
Suy ra [tex]\widehat{MDN'} = \widehat{MBN'} = \widehat{MBC} = \widehat{MDN}[/tex]
Suy ra [tex]N' \equiv N[/tex]
Khi đó, theo chứng minh trên ta có [tex]\widehat{AM'E} = \widehat{ADE} = \widehat{ACB}[/tex]
Suy ra [tex]\widehat{AME} = \widehat{ACN} \Rightarrow MNEC[/tex] nội tiếp


sr trả lời hơi muộn ạ