chứng minh trung điểm

[pejucj]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

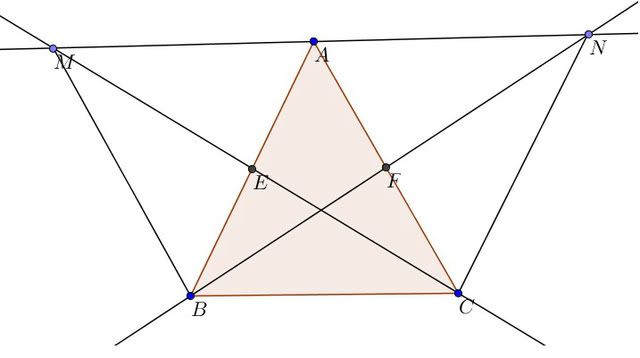
cho tam giac ABC, E la trung diem cua AB. Tren tia doi cua tia EC lay diem M sao cho EM=EC. F la trung diem cua AC, tren tia doi cua tia FB lay diem N sao cho FB=FN. Chung minh rang A la trung diem cua MN

 

[th1104]

Tự vẽ hình nha.

Ta có:

AB và MC cắt nhau tại trung điểm mỗi đường \Rightarrow MACB là hình bình hành
\Rightarrow MA = BC và MA // BC (1)

AC và MB cắt nhau tại trung điểm mỗi đường
\Rightarrow ANCB là hình bình hành

\Rightarrow AN = BC và AN//BC (2)

Từ (1) và (2) \Rightarrow A là trung điểm của MN

 

[harrypham]

Nối N với C.
Xét [TEX]\bigtriangleup FAN[/TEX] và [TEX]\bigtriangleup FCB[/TEX] có
+ [TEX]FA=FC[/TEX] (gt)
+ [TEX]FB=FN[/TEX] (gt)
+ [TEX]\widehat{FAN}= \widehat{CFB}[/TEX] (đối đỉnh)
[TEX] \Longrightarrow \bigtriangleup FAN= \bigtriangleup FBC[/TEX] (c.g.c)
[TEX]\Rightarrow AN=BC, \ \widehat{FCB}= \widehat{FAN} \Rightarrow AN//BC \ \ \ \ \ (2)[/TEX].

Nối B với M.
Xét [TEX]\bigtriangleup EAM[/TEX] và [TEX]\bigtriangleup EBC[/TEX] có
+ [TEX]EA=EB[/TEX] (gt)
+ [TEX]EM=EC[/TEX] (gt)
+ [TEX]\widehat{MEA}= \widehat{BEC}[/TEX] (đối đỉnh)
[TEX]\Rightarrow \bigtriangleup EAM= \bigtriangleup EBC[/TEX] (c.g.c)
[TEX]\Rightarrow AM=BC, \ \widehat{MAE}= \widehat{CBE} \Rightarrow AM//BC \ \ \ \ \ (2)[/TEX]


Từ (1) và (2) suy ra [TEX]MA=AN[/TEX].
[TEX]AN//BC, \ AM//BC [/TEX], theo tiên đề Ơclit, [TEX]A,N,M[/TEX] nằm trên 1 đường thẳng
[TEX]\Rightarrow A[/TEX] là trung điểm MN.