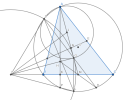
Gọi [imath]I[/imath] là giao điểm của [imath]EF[/imath] với [imath]BC[/imath], [imath]J[/imath] là trung điểm [imath]AG[/imath], [imath]P[/imath] là giao điểm của [imath]AH[/imath] với [imath](O)[/imath].
Nhận thấy [imath]G[/imath] là điểm [imath]A-humpty[/imath] của [imath]\Delta ABC[/imath] nên [imath]G \in (BHC)[/imath] và [imath]I,H,G[/imath] thẳng hàng.
Từ đó [imath]IH \cdot IG=IB \cdot IC[/imath].
Gọi [imath]L[/imath] là giao điểm [imath]IP[/imath] với [imath](O)[/imath] thì [imath]IB \cdot IC=IP \cdot IL \Rightarrow IH \cdot IG=IP \cdot IL[/imath]
Mà [imath]IH=IP \Rightarrow IG=IL[/imath]
Gọi [imath]Z'[/imath] là giao điểm khác [imath]A[/imath] của [imath](I,IG)[/imath] với [imath](J,JA)[/imath].
Ta có [imath]\widehat{LZ'G}=\dfrac{1}{2}\widehat{LIG}=\widehat{LIM}=\dfrac{1}{2}(sđLC-sđBP)[/imath]
Mà [imath]sđBP=sđDC \Rightarrow \widehat{LIM}=\dfrac{1}{2}sđLD=\widehat{LZG}[/imath]
[imath]\Rightarrow \widehat{LZ'G}=\widehat{LZG} \Rightarrow Z \in (I,IG)[/imath]
Mà [imath]Z \in (J,JA)[/imath] do [imath]\widehat{AZG}=\widehat{AZD}=90^o[/imath] và [imath]Z \in (O)[/imath] nên [imath]Z \equiv Z'[/imath](cùng là giao điểm khác [imath]A[/imath] của [imath](I,IG)[/imath] với [imath](J,JA)[/imath])
[imath]\Rightarrow IJ \perp ZG \Rightarrow IJ \parallel AT[/imath]
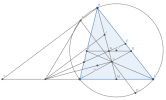
Gọi [imath]N'[/imath] là giao điểm của [imath]XY[/imath] với [imath]AM[/imath].
Ta thấy [imath]G \in AM[/imath] nên [imath]XY \parallel BC[/imath]
Áp dụng định lí Thales ta có:
[imath]\dfrac{AN'}{AM}=\dfrac{YN'}{BM}=\dfrac{YN'}{CM}=\dfrac{GN'}{GM} \Rightarrow (AG,N'M)=-1[/imath]
Mặt khác, gọi [imath]N"[/imath] là giao điểm của [imath]AM[/imath] với [imath]EF[/imath].
Ta thấy [imath]AM[/imath] là đường đối trung của [imath]\Delta AEF[/imath]. Lại có [imath]\widehat{AGH}=\widehat{AEH}=\widehat{AFH}=90^o[/imath] nên [imath]G \in (AEF)[/imath]
[imath]\Rightarrow (AG,N"M)=-1[/imath]
Suy ra [imath]N' \equiv N"[/imath] hay [imath]XY,EF,AM[/imath] đồng quy tại [imath]N[/imath].
Vì [imath](AG,NM)=-1[/imath] và [imath]J[/imath] là trung điểm [imath]AG[/imath] nên ta có [imath]MG\cdot MA=MJ \cdot MN[/imath]
[imath]\Rightarrow \dfrac{MA}{MJ}=\dfrac{MN}{MG}[/imath]
Áp dụng định lí Thales ta có: [imath]\dfrac{MT}{MI}=\dfrac{MA}{MJ}=\dfrac{MN}{MG} \Rightarrow TN \parallel IG[/imath]
[imath]\Rightarrow TN \perp AM[/imath].
Tới đây em có thể tự làm tiếp để suy ra [imath]B,C,N,P[/imath] đồng viên nhé.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
[Chuyên đề HSGQG] Một số bài toán về đa thức
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
