Toán 9 Chứng minh tính chất tứ giác nội tiếp

[Quân (Chắc Chắn Thế)]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Nguồn: Wikipedia​

Giúp em chứng minh 2 tính chất này với ạ, em cảm ơn

 

[7 1 2 5]

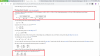
1. Vẽ AH vuông với BC, AK vuông với CD. Không mất tính tổng quát giả sử [tex]\widehat{ABC}\leq 90^o[/tex].
Áp dụng định lí Py-ta-go ta có:[tex]AC^2=AH^2+HC^2=a^2-BH^2+(b-BH)^2=a^2+b^2-2bBH=AK^2+KC^2=(d^2-DK^2)+(c+DK)^2=c^2+d^2+2cDK[/tex]
Chứng minh được [tex]\Delta ABH\sim \Delta ADK\Rightarrow \frac{BH}{DK}=\frac{AB}{AD}=\frac{a}{d}\Rightarrow BH=\frac{a.DK}{d}[/tex]
Thay vào biểu thức trên ta có:[tex]a^2+b^2-2ab.\frac{DK}{d}=c^2+d^2+2c.DK\Rightarrow \frac{DK}{d}=\frac{a^2+b^2-c^2-d^2}{2ab+2cd}\Rightarrow AC^2=c^2+d^2+2c.DK=c^2+d^2+2c.\frac{a^2+b^2-c^2-d^2}{2ab+2cd}[/tex]
Sau đó bạn thu gọn là được.
2. [tex]\frac{AE}{CE}=\frac{AE}{BE}.\frac{BE}{CE}=\frac{AD}{BC}.\frac{AB}{CD}[/tex]