S
snowangel1103
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
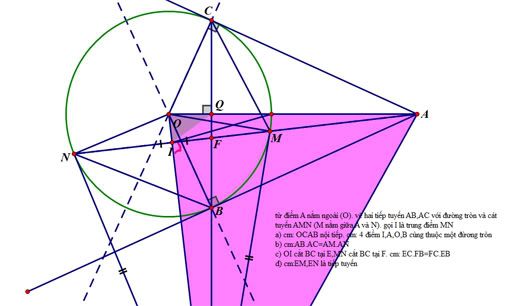
từ điểm A nằm ngoài (O). vẽ hai tiếp tuyến AB,AC với đường tròn và cát tuyến AMN (M nằm giữa A và N). gọi I là trung điểm MN
a) cm: OCAB nội tiếp. cm: 4 điểm I,A,O,B cùng thuộc một đừơng tròn
b) cm:AB.AC=AM.AN
c) OI cắt BC tại E,MN cắt BC tại F. cm: EC.FB=FC.EB
d) cm:EM,EN là tiếp tuyến
(giúp mình câu d nha. mấy câu kia mình làm đc oy.thanks)
a) cm: OCAB nội tiếp. cm: 4 điểm I,A,O,B cùng thuộc một đừơng tròn
b) cm:AB.AC=AM.AN
c) OI cắt BC tại E,MN cắt BC tại F. cm: EC.FB=FC.EB
d) cm:EM,EN là tiếp tuyến
(giúp mình câu d nha. mấy câu kia mình làm đc oy.thanks)