Toán 11 Chứng minh thẳng hàng

[Nguyễn Đăng Bình]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Giúp mình câu d với ạ.

 

[vangiang124]

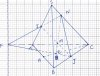
d) có [TEX]F=IN \cap AC[/TEX] [TEX]\Rightarrow \left\{\begin{matrix}F\in IN \subset (IJN) \\F\in AC \subset (ABC) \end{matrix}\right. [/TEX]

[TEX]\Rightarrow F\in (IJN)\cap(ABC)[/TEX] (1)

có [TEX]E=MN \cap CH [/TEX] [TEX]\Rightarrow \left\{\begin{matrix}E\in MN \subset(IJN) \\E\in CH \subset (ABC) \end{matrix}\right. [/TEX]

[TEX]\Rightarrow E \in (IJN)\cap (ABC) [/TEX] (2)

từ (1) và (2) suy ra [TEX](IJN)\cap (ABC)=EF[/TEX]

ngoài ra, có [TEX]J \in (IJN)\cap (ABC)[/TEX] hay [TEX]J\in EF[/TEX]
vậy [TEX]EF[/TEX] luôn đi qua điểm cố định [TEX]J[/TEX] khi [TEX]MN[/TEX] thay đổi