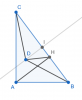
1) Ta cần chứng minh $DH^2 + HA^2 = DB^2$
$\iff DH^2 + HB \cdot HC = DB^2$ (để khử điểm $A$)
Khi đó $DB^2 - DH^2 = IB^2 - IH^2 = (IB - IH)(IB + IH) = HB \cdot HC$ nên ta có đpcm.
---
2) Để ý $a \cdot h_a = 2S = 2\sqrt{p(p-a)(p-b)(p-c)} \leqslant \sqrt{p(p-a)} \cdot (p - b + p - c) = a \sqrt{p(p-a)}$
Do đó, nhân hai vế gt cho $a$ ta có $a(2p - a) = \dfrac{a^2}2 + a \cdot h_a \cdot \sqrt{3} \leqslant \dfrac{a^2}2 + a \sqrt{3p(p - a)}$
Chuyến vế qua ta còn lại $2p - \dfrac{3}2 a \leqslant \sqrt{3p(p - a)}$
Bình phương lên, ta được $\dfrac{1}4 (2p - 3a)^2 \leqslant 0$
Như vậy dấu '=' phải xảy ra hay $a = b = c$ và ta được đpcm
Nếu bạn không hiểu chỗ nào thì có thể hỏi lại bên dưới nha. Chúc bạn học tốt!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
