Toán 9 Chứng minh tam giác đồng dạng bằng tâm đường tròn khó

[Nguyen Ngoc Lam]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

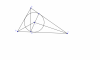
Cho [TEX]\triangle[/TEX]ABC. Gọi I là tâm của đường tròn nội tiếp [TEX]\triangle[/TEX]ABC. Từ I vẽ đường thẳng vuông góc với CI cắt AB và AC lần lượt tại M và N
a) Chứng minh [TEX]\triangle[/TEX]AMI ~ [TEX]\triangle[/TEX]AIB
b) Chứng minh AM . BN = IM2 = IN2
c) Chứng minh [TEX]\frac{IA^2}{AC.AB}[/TEX]+[TEX]\frac{IB^2}{AB.BC}[/TEX]+[TEX]\frac{IC^2}{BC.AC}[/TEX]

 

[Tư Âm Diệp Ẩn]

a) Ta có:[tex]\angle AMI=\angle MIC+\angle MCI[/tex]
Mà: [tex]\angle MCI=ICN[/tex](tính chất hai tiếp tuyến)
[tex]\rightarrow \angle AMI=90^{o}+\angle ICN[/tex]
Tương tự: [tex]\angle INB=\angle NIC+\angle ICN=90^{o}+\angle ICN\\ \angle AIB=180^{o}-\frac{1}{2}\angle BAC-\frac{1}{2}\angle ABC=180^{o}-\frac{1}{2}(180^{o}-\angle ACB )=90^{o}+\angle ICN[/tex]
[tex]\rightarrow \angle AMI=\angle INB=\angle AIB[/tex]
Xét [tex]\triangle AMI[/tex] và [tex]\triangle AIB[/tex] có: [tex]\angle MAI=\angle IAB;\angle AIB=\angle AMI[/tex]
[tex]\rightarrow \triangle AMI[/tex] ~[tex]\triangle AIB[/tex] (g-g)
b) Chứng minh tương tự a, được [tex]\triangle AIB[/tex]~[tex]\triangle INB\rightarrow \frac{IN}{BN}=\frac{AN}{IN}\rightarrow AN.BN=IM^2=IN^2[/tex] (Dễ dàng chứng minh IM = IN)
c) Đặt AM= m, BN=n; IM=IN=x ; BC=a; AC=b; AB=c
Theo a, [tex]\triangle AIB[/tex]~[tex]\triangle AMI\rightarrow \frac{AM}{AI}=\frac{AI}{AB}\rightarrow AI^2=AM.AB=mc\rightarrow \frac{IA^2}{bc}=\frac{m}{b}[/tex] (1)
Tương tự, [tex]\triangle AIB[/tex]~[tex]\triangle INB\rightarrow \frac{AB}{IB}=\frac{IB}{NB}\rightarrow IB^2=AB.NB=cn\rightarrow \frac{IB^2}{ca}=\frac{n}{a}[/tex] (2)
Xét [tex]\triangle MIC: IC^2=MC^2-NC^2[/tex]
Theo a, ta có: [tex]IM^2=AM.AN[/tex] và [tex]CM=CN[/tex]
[tex]\rightarrow IC^2=CM.CN-AM.AN=(b-m)(a-n)-mn=ab-bn-am[/tex]
[tex]\rightarrow \frac{IC^2}{ab}=\frac{ab-bn-am}{ab}=1-\frac{n}{a}-\frac{m}{b}[/tex] (3)
Từ (1); (2) và (3) ta có:
[tex]\frac{IA^2}{bc}+\frac{IB^2}{ca}+\frac{IC^2}{ab}=1[/tex] hay: [tex]\frac{IA^2}{AC.AB}+\frac{IB^2}{AB.BC}+\frac{IC^2}{AC.BC}=1[/tex]