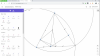
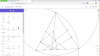
Mình nhìn hình của bạn
@Quân (Chắc thế) rối quá nên vẽ lại
, và đây mới là câu a thôi nha
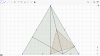
Nối A với D. Vì D là đường trung tuyến của tam giác ABC, mà tam giác ABC đều nên AD đồng thời là tia phân giác của [tex]\widehat{BAC}[/tex] và cũng là đường cao.
[tex]\Rightarrow \widehat{BAD}=\frac{1}{2}\widehat{BAC}=60^o.\frac{1}{2}=30^o[/tex] .
Vì AD là đường cao nên [tex]AD\perp BC\Rightarrow \widehat{ADB}=90^o[/tex] hay [tex]\widehat{ADM}=90^o[/tex].
Xét[tex]\Delta ADM[/tex] vuông tại D có I là trung điểm cạnh huyền AM nên DI là đường trung tuyến ứng với cạnh huyền thì bằng 1 nửa cạnh huyền
[tex]\Rightarrow DI=\frac{1}{2}AM=AI=IM[/tex] (1)
[tex]DI=AI\Rightarrow[/tex] [tex]\Delta AID[/tex] cân tại I[tex]\Rightarrow \widehat{IAD}=\widehat{IDA}\Rightarrow \widehat{IAD}+\widehat{IDA}=2.\widehat{IAD}[/tex] .(2)
Vì [tex]\widehat{DIM}[/tex] là góc ngoài tại đỉnh I của [tex]\Delta DIA\Rightarrow \widehat{DIM}=\widehat{IAD}+\widehat{IDA}=2.\widehat{IAD}[/tex].
Phần này mình ngại gõ nên viết như sau, vì nó chứng minh giống phần trên thôi, chỉ khác tam giác:
Đối với [tex]\Delta MPA[/tex] thì cũng là tam giác vuông nên [tex]IP=IA=IM[/tex](3) và[tex]\widehat{PIM}=\widehat{IAP}+\widehat{IPA}[/tex]=[tex]=2.\widehat{IAP}[/tex](4)
Từ (1) và (3)[tex]\Rightarrow[/tex] [tex]ID=IP[/tex][tex]\Rightarrow \Delta DIP[/tex] cân tại I(5)
Cộng theo từng vế của (2) và (4) ta được:[tex]\widehat{DIM}+\widehat{PIM}[/tex]=[tex]2.\widehat{DAI}+2.\widehat{PAI}=2.(\widehat{DAI}+\widehat{PAI})=2.\widehat{BAD}=2.30^o=60^o[/tex] hay [tex]\widehat{DIP}=60^o[/tex](6)
Từ (5) và (6)[tex]\Rightarrow[/tex] [tex]\Delta PID[/tex] đều.
Chúc bạn học tốt!^^
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
