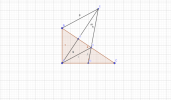
Cho tam giác ABC vuông tại A có AH là đường cao, AB < AC. AD là tia phân giác góc HAC, D thuộc HC. Cho M là trung điểm của AC, E là giao điểm của AH và MD. Chứng minh : EB // AD.
Giúp em với ạ, e cảm ơn
View attachment 217487
Xia Hoa Tuyết
Xét [imath]\Delta ADC[/imath] có [imath]\dfrac{MA}{MC}.\dfrac{DC}{DH}.\dfrac{EH}{EA}=1\Rightarrow \dfrac{DC}{DH}=\dfrac{EA}{EH}[/imath]
Dễ dàng CM [imath]\Delta ABH\sim \Delta CAH\Rightarrow \dfrac{AB}{BH}=\dfrac{AC}{AH}[/imath]
Mà [imath]\widehat{BAD}=\widehat{BAH}+\widehat{HAD}=\widehat{ACB}+\widehat{DAC}=\widehat{BDA}[/imath]
[imath]\Rightarrow \Delta ABD[/imath] cân tại [imath]B\Rightarrow AB=BD[/imath]
Suy ra [imath]\dfrac{BD}{BH}=\dfrac{AC}{AH}=\dfrac{DC}{DH}[/imath] (tc đường phân giác)
Suy ra [imath]\dfrac{BD}{DH}=\dfrac{EA}{EH}\Rightarrow \dfrac{BH}{HD}=\dfrac{AH}{HE}[/imath]
[imath]\Rightarrow \Delta HAD\sim \Delta HEB\Rightarrow \widehat{HAD}=\widehat{HEB}\Rightarrow AD//BE[/imath]
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Ôn tập toán các dạng bài hình học 9
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.