- 4 Tháng bảy 2021
- 1,211
- 5,487
- 491
- 18
- Long An
- Trường THCS Thị Trấn Đông Thành
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Giúp em câu d) với ạ. Em cảm ơn! Huhu, em nghĩ ko ra mặc dù tìm được hướng giải
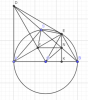
Cho đường tròn tâm (O) đường kính AB, S là một điểm thuộc đường tròn sao cho SA<SB. Tiếp tuyến tại A của (O) cắt BS tại D. Vẽ dây $AE\perp OD$ tại F.
a. Chứng minh tam giác ASB vuông
b. Chứng minh A,F,D,S thuộc một đường tròn
c. Chứng minh DE là tiếp tuyến của (O)
d. Đường thẳng qua E vuông với AB tại K cắt BS tại N. Chứng minh: $NF\parallel AB$
@Cáp Ngọc Bảo Phương , @vangiang124 , @Timeless time
Cho đường tròn tâm (O) đường kính AB, S là một điểm thuộc đường tròn sao cho SA<SB. Tiếp tuyến tại A của (O) cắt BS tại D. Vẽ dây $AE\perp OD$ tại F.
a. Chứng minh tam giác ASB vuông
b. Chứng minh A,F,D,S thuộc một đường tròn
c. Chứng minh DE là tiếp tuyến của (O)
d. Đường thẳng qua E vuông với AB tại K cắt BS tại N. Chứng minh: $NF\parallel AB$
@Cáp Ngọc Bảo Phương , @vangiang124 , @Timeless time
Attachments
Last edited by a moderator: