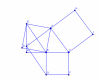
Cho $\triangle ABC$ và các hình vuông $ABED$, $ACIH$, $BCGF$. Chứng minh rằng $\overrightarrow{AD}+\overrightarrow{BF}+\overrightarrow{CH}=\overrightarrow0$
View attachment 195606
Dựng hình bình hành $EBGJ$. $BC$ cắt đường thẳng $EJ$ tại $K$.
Ta có $EJ\parallel BG$ và $BG\perp BC\Rightarrow EJ\perp BC\Rightarrow \widehat{EKB}=90^\circ$
Ta cũng có $\widehat{EAB}=90^\circ$ nên $AEBK$ nội tiếp $\Rightarrow \widehat{KEA}=\widehat{ABC}$
Chứng minh được $\triangle AEJ=\triangle ABC$ (c.g.c) $\Rightarrow AJ=AC;\widehat{EAJ}=\widehat{BAC}$
$\widehat{EAJ}=\widehat{BAC}\Leftrightarrow \widehat{EAJ}+\widehat{JAB}=\widehat{BAC}+\widehat{JAB}\Leftrightarrow \widehat{EAB}=\widehat{JAC}\Leftrightarrow \widehat{JAC}=90^\circ\Rightarrow JA\parallel IC$
Ta chỉ ra $\overrightarrow{EJ}=\overrightarrow{BG};\overrightarrow{JA}=\overrightarrow{CI}$
Áp dụng quy tắc hình bình hành:
$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{AE}$
$\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{BG}=\overrightarrow{BC}+\overrightarrow{EJ}$
$\overrightarrow{CH}=\overrightarrow{CA}+\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{JA}$
$\Rightarrow \overrightarrow{AD}+\overrightarrow{BF}+\overrightarrow{CH}=\overrightarrow{AB}+\overrightarrow{AE}+\overrightarrow{BC}+\overrightarrow{EJ}+\overrightarrow{CA}+\overrightarrow{JA}\\=(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA})+(\overrightarrow{AE}+\overrightarrow{EJ}+\overrightarrow{JA})=\overrightarrow0$
Nếu có thắc mắc, bạn cứ hỏi tại đây, tụi mình sẽ hỗ trợ.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
