View attachment 186448
Trước hết, mình chỉ hướng cho bài này nhé:
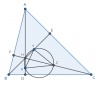
Đầu tiên mình nhìn vô biểu thức, mình thấy nó giống giống: $$\dfrac{HD}{AD} + \dfrac{HE}{BE} + \dfrac{HF}{CF} = 1$$ nên thay vô rồi rút gọn. Có một vấn đề là tùy theo hình vẽ mà nó sẽ ra khác nhau. Ở đây mình giả sử hình vẽ giống như trên.
Khi đó mình sẽ thu được: $\dfrac{HZ}{CF} = \dfrac{HX}{AD} + \dfrac{HY}{BE} \, (1)$.
Nhìn thấy các tỉ lệ như thế này, mình nghĩ là có thể sẽ liên hệ tới tam giác đồng dạng, sau đó chứng minh góc bằng nhau rồi suy ra tứ giác nội tiếp. Ở đây, quan sát thấy tam giác $XYZ$ đồng dạng tam giác $ABC$, nhưng dường như cạnh $YZ$ và $XZ$ hơi khó liên hệ tới.
Vậy có cách nào không?
Tự dưng mình nghĩ tới định lý Ptolemy: Ta đi chứng minh $$HZ \cdot XY = HX \cdot YZ + HY \cdot XZ$$
Nhìn biểu thức này quen quen nhỉ...
Đúng rồi, nó là $(1)$. Vậy từ $(1)$ ta biến đổi sao cho nó thành dạng tích giống vậy, bằng cách nhân hai vế cho $2S$ hay hai lần diện tích: $$HZ \cdot AB = HX \cdot BC + HY \cdot AC$$
Như vậy ta chỉ cần chứng minh tỉ lệ $AB : BC : AC = XY : YZ : XZ$ là xong, mà đây lại là tỉ lệ của hai tam giác đồng dạng ta nói đến ở trên! Như vậy, để chứng minh tứ giác nội tiếp thì ta cần chứng minh tam giác đồng dạng, mà để chứng minh tam giác đồng dạng này ta lại cần đến góc của tứ giác nội tiếp...
Vậy có cách nào giải quyết không?
Một cách đó là: Ta sử dụng điểm trùng. Giả sử có điểm $Z'$ mới sao cho tứ giác nội tiếp và đồng dạng, ta chứng minh $Z \equiv Z'$ bằng tỉ lệ ban đầu. Vậy là đã... xong?
Umm, thật ra lời giải này phụ thuộc rất nhiều vào hình vẽ. Chẳng hạn, tại sao $XYZ$ lại có vị trí như hình? Chẳng hạn $Y$ thuộc $HB$ thì sao? Rồi khi $Z'$ thỏa mãn tỉ lệ như trên thì liệu nó có thật sự trùng $Z$?
Bạn có thể suy nghĩ thử
Nhưng ý tưởng thì mình nghĩ, cách làm trên khá phù hợp với bài toán rồi nên mình xin phép để lại phần còn lại cho bạn nhé
Nếu có thắc mắc thì bạn có thể hỏi bên dưới. Chúc bạn học tốt!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
