Vẽ đường kính [imath]AD[/imath]. Khi đó ta dễ thấy rằng [imath]DM=MH[/imath] nên [imath]DMNR[/imath] cũng là hình bình hành.
Từ đó [imath]MN \parallel DR[/imath] nên ta sẽ chứng minh [imath]DR \perp KL[/imath].
Gọi [imath]T[/imath] là giao điểm của [imath]KE[/imath] và [imath]LF[/imath]. Đường thẳng qua [imath]A[/imath] vuông góc với [imath]AT[/imath] cắt [imath]BC[/imath] tại [imath]S[/imath]. [imath]AP[/imath] cắt [imath]BC[/imath] tại [imath]I[/imath].
Vẽ tia [imath]Tx \parallel EF[/imath] như hình.
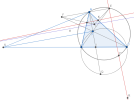
Khi đó ta thấy [imath](TE,TF,TA,Tx)=\dfrac{\overline{AE}}{\overline{AF}}[/imath].
Mà [imath]AC \perp TE, AB \perp TF, AS \perp TA, AP \perp Tx[/imath] nên [imath](AC,AB,AS,AP)=(TE,TF,TA,Tx)[/imath]
[imath]\Rightarrow (CB,SI)=(TE,TF,TA,Tx)[/imath]
[imath]\Rightarrow P(CB,SI)=(TE,TF,TA,Tx)[/imath]
[imath]\Rightarrow P(CB,SI)=\dfrac{\overline{AE}}{\overline{AF}}[/imath]
[imath]\Rightarrow P(FE,SA)=\dfrac{\overline{AE}}{\overline{AF}}[/imath]
[imath]\Rightarrow PS \parallel EF \Rightarrow PS \perp AP[/imath]
Vẽ tia [imath]Ay \perp KL[/imath] thì ta cần chứng minh [imath]DR \parallel Ay[/imath]
[imath]\Leftrightarrow \widehat{yAR}=\widehat{ARD}[/imath]
Mặt khác, do [imath]ALTK[/imath] nội tiếp đường tròn đường kính [imath]AT[/imath] nên [imath]Ay[/imath] đẳng giác với [imath]AT[/imath] trong [imath]\widehat{LAK}[/imath]
[imath]\Rightarrow \widehat{yAR}=\widehat{TAP}=90^o-\widehat{SAT}=\widehat{ASP}[/imath]
Ta thấy [imath]\widehat{BAP}=\widehat{RAC},\widehat{RCA}=180^o-\widehat{QCB}=180^o-\widehat{QPB}=\widehat{APB}[/imath] nên [imath]\Delta ABP \sim \Delta ARC[/imath]
Trên đường thẳng [imath]PS[/imath] ta lấy điểm [imath]J[/imath] sao cho [imath]\widehat{BAJ}=\widehat{RAD}[/imath]
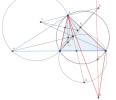
Ta thấy [imath]PJ \perp AP, DC \perp AC[/imath] và [imath]\widehat{BAJ}=\widehat{RAD}[/imath] nên [imath]J,D[/imath] là [imath]2[/imath] điểm tương ứng nhau trong [imath]\Delta ABP[/imath] và [imath]\Delta ARC[/imath]
[imath]\Rightarrow \widehat{ABJ}=\widehat{ARD}[/imath].
Từ đó ta chỉ cần chứng minh [imath]\widehat{ABJ}=\widehat{ASP}[/imath] hay [imath]ASBJ[/imath] nội tiếp.
Ta có: [imath]\widehat{BAJ}=\widehat{RAD}=\widehat{HAP}[/imath] (do [imath]AR,AP[/imath] và [imath]AH,AD[/imath] là cặp đường đẳng giác trong [imath]\widehat{BAC}[/imath])
[imath]=90^o-\widehat{AIB}=\widehat{BSJ}[/imath]
Từ đó [imath]ASBJ[/imath] nội tiếp hay ta có điều phải chứng minh.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.



