[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
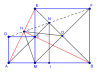
Cho đoạn thẳng AB và điểm M tùy ý trên đó. Trên cùng nửa mặt phẳng bờ AB; vẽ các hình vuông AMCD và BMEF.
a) Chứng minh AE vuông góc BC
b) Gọi H là giao điểm của AE và BC. CHứng minh D, H, F thẳng hàng
c) Chứng minh khi M di chuyển trên AB thì DF luôn đi qua một điểm cố định
a) Chứng minh AE vuông góc BC
b) Gọi H là giao điểm của AE và BC. CHứng minh D, H, F thẳng hàng
c) Chứng minh khi M di chuyển trên AB thì DF luôn đi qua một điểm cố định