Toán Chứng minh hình học

[trunghieule2807]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

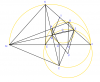
Cho đường tròn O và điểm M nằm ngoài đường tròn. Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm ; A nằm giữa hai điểm M và B; A và C nằm khác phía đối với đường thẳng MO).
1) Chứng minh rằng MA.MB=ME.MF.
2) Gọi H là hình chiếu vuông góc với điểm C trên đường thẳng MO. Chứng minh rằng AHOB là tứ giác nội tiếp.
3) Trên nửa mặt phẳng bờ là đường thẳng OM có chứa điểm A, vẽ nửa đường tròn đường kính MF. Nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi giao điểm của hai đường thẳng CO và KF. Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.
4) Gọi P, Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS, ABS và T là trung điểm của KS. Chứng minh rằng ba điểm P, Q, T thẳng hàng.
r107r107 Nếu thích thì like nhér107r107

 

[Phương Trang]

a) xét [tex]\Delta MEB[/tex] và [tex]\Delta MAF[/tex] , có:
[tex]\widehat{M}[/tex] chung
[tex]\widehat{EFA} = \widehat{EBA}[/tex] ( cùng chắn cung EA)
=> [tex]\Delta MEB \sim \Delta MAF[/tex]
=> [tex]\frac{ME}{MA} = \frac{MB}{MI}[/tex]
=>MF.MB= MA.MB

 

[Phương Trang]

b) [tex]\Delta MCA \sim \Delta MBC[/tex] (g-g)
=> [tex]\frac{MC}{MB} = \frac{MA}{MC}[/tex]
=> [tex]MC^{2}[/tex] =MA.MB
[tex]\Delta MCO[/tex] vuông tại C, CH đường cao : [tex]MC^{2}[/tex] = MH. MO
Do đó : MA. MB = MH. MO
Suy ra : [tex]\Delta MHA \sim \Delta MBO[/tex] (c-g-c)
=> [tex]\widehat{MHA} = \widehat{MBO}[/tex]
=> AHOB nội tiếp ( tứ giác có góc trong bằng góc đối ngoài)

 

[iceghost]

1/ Dễ thấy $MC^2 = MA \cdot MB$ và $MC^2 = ME \cdot MF \longrightarrow$ đpcm
2/ Dễ thấy $MC^2 = MH \cdot MO$ và $MC^2 = MA \cdot MB \implies MH \cdot MO = MA \cdot MB$
Sau đó đi CM $\triangle{MAH} \sim \triangle{MOB} \implies \widehat{MAH} = \widehat{MOB}$
Suy ra $AHOB$ nt
3/ Dễ thấy $MK^2 = ME \cdot MF$ và $MC^2 = ME \cdot MF \implies MK = MC$
Sau đó đi CM $\triangle{MKS} = \triangle{MCS} \implies SC = SK$
Từ $MK = MC$ và $SC = SK$ suy ra $MS$ là đường trung trực của $CK$, suy ra $MS \perp CK$
4/ Gọi $R$ là giao của $MS$ và $CK$
Dễ thấy $MC^2 = MR \cdot MS$ và $MC^2 = MA \cdot MB$ và $MC^2 = ME \cdot MF$
$\implies MR \cdot MS = MA \cdot MB$ và $MR \cdot MS = ME \cdot MF$
Sau đó CM $ABSR$ và $EFSR$ nt như câu b, suy ra $(P)$ và $(Q)$ đi qua $R$.
Khi đó $P, Q, T$ đều thuộc đường trung trực của $RS$ nên ta có đpcm

 

[trunghieule2807]

*Hình vẽ chèn sau*
1/ Dễ thấy $MC^2 = MA \cdot MB$ và $MC^2 = ME \cdot MF \longrightarrow$ đpcm
2/ Dễ thấy $MC^2 = MH \cdot MO$ và $MC^2 = MA \cdot MB \implies MH \cdot MO = MA \cdot MB$
Sau đó đi CM $\triangle{MAH} \sim \triangle{MOB} \implies \widehat{MAH} = \widehat{MOB}$
Suy ra $AHOB$ nt
3/ Dễ thấy $MK^2 = ME \cdot MF$ và $MC^2 = ME \cdot MF \implies MK = MC$
Sau đó đi CM $\triangle{MKS} = \triangle{MCS} \implies SC = SK$
Từ $MK = MC$ và $SC = SK$ suy ra $MS$ là đường trung trực của $CK$, suy ra $MS \perp CK$
4/ Gọi $R$ là giao của $MS$ và $CK$
Dễ thấy $MC^2 = MR \cdot MS$ và $MC^2 = MA \cdot MB$ và $MC^2 = ME \cdot MF$
$\implies MR \cdot MS = MA \cdot MB$ và $MR \cdot MS = ME \cdot MF$
Sau đó CM $ABSR$ và $EFSR$ nt như câu b, suy ra $(P)$ và $(Q)$ đi qua $R$.
Khi đó $P, Q, T$ đều thuộc đường trung trực của $RS$ nên ta có đpcm

Đoạn câu 4 bạn viết lại cho dễ nhìn được không mình không hiểu lắm

 

[iceghost]

Đoạn câu 4 bạn viết lại cho dễ nhìn được không mình không hiểu lắm

Bạn không hiểu chỗ nào nhỉ ?

 

[trunghieule2807]

Xin lỗi mình nhầm là do máy lag