Toán 8 Chứng minh HF = AB - BC với điều kiện cho trước

[nguyen van ut]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho hình bình hành ABCD. Các tia phân giác góc A,B,C,D cắt nhau như hình trên .CM: HF=AB-BC

 

[nhu20071978@gmail.com]

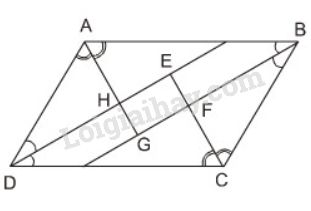
Ta có: ABC+BCD=180
=>BFC+FCB=90
=>CFB=90
=>BF vuông góc với CF.CM tương tự,AG vuông có với BF=>AG song song vớiCF
gọi giao điểm của CF với AB là M=>AH song song với MF(1*)
Tam giác BMC có BF vừa là đường cao vừa là đường phân giác
=>tam giác BMC cân tại B
=>BM=BC=>AB-BC=AB-BM=AM(1**)
Mặt khác,tam giác BMC cân=>BF là đường trung tuyến của tam giác BMC=>MF=FC(1)
Xét tam giác ADH và tam giác CBF có:
ADH=FBC(D/2=B/2)
AD=BC
DAH=FCB(A/2=C/2)
=> tam giác ADH=tam giác CBF(g-c-g)
=>AH=CF(2)
Từ (1) và (2)=>MF=AH(2*)
Từ (1*) và (2*)=> tứ giác AMFH là hình bình hành=>AM=HF(2**)
Từ(1**) và (2**)=>AB-BC=HF(ĐPCM)
p/s:mình không biết chỗ kí hiệu góc nên bạn tự hiểu nhé!