Toán 9 Chứng minh góc bằng nhau và chứng minh trung điểm của đoạn thẳng

[Junery N]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Giúp mình/em câu b và câu c

 

[Nguyễn Linh_2006]

View attachment 175130
Giúp mình/em câu b và câu c

Làm được câu b thoi :3 Câu c nhờ cao nhân @kido2006 nè <3
____________________________________



[tex]H[/tex] đối xứng [tex]M[/tex] qua [tex]D[/tex] [tex]\rightarrow CH=CM\rightarrow \widehat{MCB}=\widehat{BCT}[/tex]

Xét [tex](O): \widehat{BAM}=\widehat{BCM}[/tex] (góc nội tiếp cùng chắn một cung)

Do đó : [tex]\rightarrow \widehat{BCT}=\widehat{BAD}[/tex]

[tex]\rightarrow \widehat{BCT}+\widehat{TBC}=\widehat{BAD}+\widehat{ABD}=90^{\circ}[/tex]

[tex]\rightarrow \widehat{BTC}=90^{\circ}\rightarrow BT\perp TC[/tex]

CM : [tex]H[/tex] là trực tâm [tex]\Delta ABC[/tex]

Dễ dàng CM : [tex]BTSC[/tex] nội tiếp [tex]\rightarrow \widehat{BST}=\widehat{BCT}[/tex]

 

[kido2006]

View attachment 175130
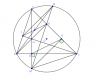
Giúp mình/em câu b và câu c

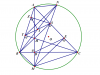
c, Dựng SZ vuông góc với AB
Ta có [tex]BZ.BA=BS^2[/tex] (hệ thức lượng )
Có [tex]\Delta BIS\sim \Delta BSN(g.g)[/tex] [tex]\Rightarrow BN.BI=BS^2[/tex]
[tex]\Rightarrow BZ.BA=BI.BN[/tex]
[tex]\Rightarrow ZANI[/tex] nội tiếp
[tex]\Rightarrow \widehat{TZI}=\widehat{ANB}[/tex]
Mà [tex]\widehat{ANB}=\widehat{ACB}=\widehat{ZTI}[/tex]
[tex]\Rightarrow \widehat{TZI}=\widehat{ZTI}\Rightarrow IT=IZ[/tex]
Từ [tex]\widehat{TZI}=\widehat{ZTI}\Rightarrow \widehat{ISZ}=\widehat{IZS}\Rightarrow IS=IZ[/tex]
[tex]\Rightarrow IT=IS[/tex]



__
Cách khác không phải kẻ thêm
Dễ thấy [tex]\left\{\begin{matrix} \Delta SHD\sim \Delta STB(g.g) \\ \Delta SHM\sim \Delta ITB(g.g) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} HD.ST=SH.TB\\ IT.HM=SH.TB \end{matrix}\right. \Rightarrow HD.ST=IT.HM\Rightarrow 2TI=ST\Rightarrow đpcm[/tex]