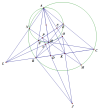
Gọi EF cắt BC tại L, đường tròn đường kính AH cắt đường trồn tại N khác A
Hiển nhiên có A,N,L thẳng hàng (bạn có thể chứng minh bằng tâm đẳng phương-rất ngắn)
Gọi AO cắt O tại M khác A ; DJ cắt EF tại P; AM cắt EF tại U
Ta chỉ cần chứng minh 3 điểm P H M thẳg hàng là được đpcm
Thật vậy cũng hiển nhiên có N,H,K,M thẳng hàng (sử dụng các góc nội tiếp chắn nửa đường tròn)
Do đó bài toán lại quy về chứng minh [imath]\widehat{ANP}=90[/imath]
Mặt khác ta có [imath]\widehat{AUE}=180-\widehat{AEU}-\widehat{EAU}=180-\widehat{ABC}-\widehat{MBC}=180-\widehat{ABM}=90[/imath]
Gọi OL cắt PJ tại V
Ta có FDKE nội tiếp (bạn sử dụng góc)
=> [imath]\widehat{EDK}=\widehat{FDB}=\widehat{LEK}[/imath]
=> [imath]\Delta LKE \sim \Delta EKD[/imath]
=> [imath]DK.LK=EK^2=BK^2=KO.KJ[/imath]
=> [imath]\Delta LOK \sim \Delta JDK[/imath]
=> [imath]DJ \perp OL[/imath]
=> DVOK là tứ giác nội tiếp và PVOU là tứ giác nội tiếp
=> [imath]LP.LU=LV.LO=LD.LK=LF.LE=LN.LA[/imath]
=> ANPU nội tiếp
=> [imath]\widehat{ANP}=90[/imath]
Do đó ta được điều phải chứng minh
 Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé.
Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nhé
Ôn tập hình học lớp 9
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


