 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
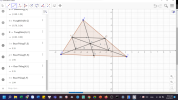 định lý:
định lý:Cho tam giác [imath]\Delta ABC[/imath] bất kì, vẽ các đường trung tuyến [imath]AD, BE, CF.[/imath]
Gọi G là trong tâm, ta có:[imath]AG = 2GD[/imath];[imath]AD = 3GD[/imath];[imath]AD = \frac{3}{2} AG[/imath]
HÌnh vẽ:
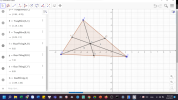
Cách chứng minh:
Gọi [imath]I[/imath] là trung điểm của [imath]GB, K[/imath] là trung điểm của [imath]GC[/imath]
Nối các điểm: [imath]I-K-E-F[/imath]
Sử dụng tính chất đường trung bình cho [imath]\Delta ABC[/imath] và cạnh [imath]EF[/imath], ta có [imath]EF = \dfrac{BC}{2}[/imath] (1)
Sử dụng tính chất đường trung bình cho [imath]\Delta GBC[/imath] và cạnh IK, ta có [imath]IK = \dfrac{BC}{2}[/imath] (2)
[imath](1),(2) \to EF = IK[/imath]
Sử dụng tính chất đường trung bình cho [imath]\Delta ABG[/imath] và cạnh [imath]FI[/imath], ta có [imath]FI = \dfrac{AG}{2}[/imath] (3)
Sử dụng tính chất đường trung bình cho [imath]\Delta GAC[/imath] và cạnh [imath]EK[/imath], ta có [imath]EK = \dfrac{AG}{2}[/imath] (4)
[imath](3),(4) \to FI = EK[/imath]
ảnh:

So sánh [imath]\Delta FEI[/imath] và [imath]\Delta KIE[/imath] ta có [imath]\Delta FEI = \Delta KIE \to \widehat{FEI} = \widehat{KIE}[/imath]
(xài tạm để chỉ góc)
So sánh [imath]\Delta EFK[/imath] và [imath]\Delta IKF[/imath] ta có [imath]\Delta EFK = \Delta IKF \to \widehat{EFK} = \widehat{FKI}[/imath]
So sánh [imath]\Delta FEG[/imath] và [imath]\Delta KIG[/imath] ta có [imath]\Delta FEG = \Delta KIG \to FG = GK[/imath]
mà [imath]GK = CK (gt) \to FG = GK = CK[/imath]
[imath]\to GC = 2 FG ; FC = 3 FG ; FC = \frac{3}{2}GC[/imath]
(có thể sử dụng hình bình hành)
(tự chứng minh các đường trung tuyến còn lại)
Last edited by a moderator:

