Chứng minh tính chất của ba đường trung tuyến của một tam giác là đúng
Cho tam giác ABC, điểm D, E, F là trung điểm tương ứng của AB, BC và AC và G là trọng tâm
Từ F vẽ đường thẳng song song với DC, cắt AB tại Q
Hai tam giác ADC và AQF đồng dạng, suy ra được AQ:AD = AF:AC = 1:2 nên Q sẽ là trung điểm của AD. Đặt P là trung điểm DB, tỉ số QD
B sẽ bằng 1:2
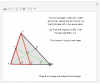
Hai tam giác QBF và DBG đồng dạng, suy ra FG:GB = QD
B = 1:2.
Chứng minh tương tự với 2 đường trung tuyến còn lại.
Nói theo cách khác, khoảng cách từ đỉnh đến trọng tâm gấp đôi khoảng cách từ trọng tâm đến trung điểm cạnh đối diện, hay khoảng cách đường trung tuyến đến đỉnh bằng 2/3 độ dài đường trung tuyến ấy.
Hình ảnh mình lấy từ:
demonstrations.wolfram.com/TheCentroidOfATriangleDividesEachMedianInTheRatio12/
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
