Toán 11 Chứng minh đi qua 1 điểm

[Nguyễn Đăng Bình]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

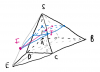
Cho hình chóp SABCD có đáy ABCD là hình thang (AB // CD, AB > CD). Gọi M, N lần lượt là trung điểm SA, SB. P là một điểm di chuyển trên cạnh SC . Gọi Q là giao của SD và mp(MNP). Tìm quỹ tích giao điểm I của MQ và NP, giao điểm J của MP, NQ. CMR IJ luôn đi qua một điểm cố định.

 

[iceghost]

Bạn tham khảo hình vẽ bên dưới.

$I \in MQ \subset (SAE)$ và $I \in NP \subset (SBE)$ nên $I \in (SAE) \cap (SBE) = SE$

Tương tự, $J \in SO = (SAC) \cap (SBD)$

Tới đây, nhận xét $IJ = (SOE) \cap (MNPQ)$

Do $MN \subset (MNPQ)$ và $SK \subset (SOE)$ nên $MN \cap SK \in (MNPQ) \cap (SOE) = IJ$

Đây cũng chính là điểm cố định mà ta cần tìm

Nếu bạn có câu hỏi nào thì bạn hãy hỏi bên dưới nhé. Chúc bạn học tốt!

 

[7 1 2 5]

Xét [TEX](SAB),(SDC),(ABCD)[/TEX] đôi một có giao tuyến là [TEX]AB,CD,d[/TEX] trong đó [TEX]d[/TEX] là giao tuyến của [TEX](SAB),(SDC)[/TEX] nên đi qua S.
Khi đó vì [TEX]AB//CD[/TEX] nên [TEX]d//AB//CD[/TEX].
Xét [TEX](SAB),(SDC),(MNPQ)[/TEX] đôi một có giao tuyến là [TEX]MN,PQ,d[/TEX] mà [TEX]d//AB//MN[/TEX] nên [TEX]d//MN//PQ[/TEX] hay [TEX]PQ//CD[/TEX]
Vẽ [TEX]AD[/TEX] cắt [TEX]BC[/TEX] tại H thì [TEX]SH[/TEX] là giao tuyến của [TEX](SAD),(SBC)[/TEX], mà [TEX]MQ,NP[/TEX] thuộc [TEX](SAD),(SBC)[/TEX] nên [TEX]I[/TEX] nằm trên [TEX]SH[/TEX]. Qũy tích của [TEX]I[/TEX] là [TEX]SH[/TEX]
Lại có theo bổ đề hình thang thì [TEX]IJ[/TEX] đi qua trung điểm [TEX]MN[/TEX] cố định.

 

[Nguyễn Đăng Bình]

Bạn tham khảo hình vẽ bên dưới.

$I \in MQ \subset (SAE)$ và $I \in NP \subset (SBE)$ nên $I \in (SAE) \cap (SBE) = SE$

Tương tự, $J \in SO = (SAC) \cap (SBD)$

Tới đây, nhận xét $IJ = (SOE) \cap (MNPQ)$

Do $MN \subset (MNPQ)$ và $SK \subset (SOE)$ nên $MN \cap SK \in (MNPQ) \cap (SOE) = IJ$

Đây cũng chính là điểm cố định mà ta cần tìm

Nếu bạn có câu hỏi nào thì bạn hãy hỏi bên dưới nhé. Chúc bạn học tốt!


View attachment 187745

G/s gọi điểm đó là L thì L là trung điểm MN đúng không ạ?
Nếu đúng là vầy thì anh chứng minh giúp em với :<