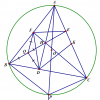
cho tam giác abc nội tiếp đường tròn (O,R) có các đường cao AD,BE,CF cắt nhau tại H. gọi k là trung điểm AC.
a/cmr D,K,E.F nằm trên cùng 1 đường tròn.
b/cmr: DF<=2OK
_______________________________________________________________
a) Dễ dàng chứng minh được: $AFHE;BFHD$ nội tiếp
Ta có: [tex]\widehat{EFH}=\widehat{HAE};\widehat{HFD}=\widehat{HBD}[/tex]
Mà: [tex]\widehat{HAE}=\widehat{HBD}[/tex]
[tex]\Rightarrow \widehat{EFH}=\widehat{HFD}=\widehat{HAE}=\widehat{HBD}[/tex]
[tex]\Rightarrow 2\widehat{EFH}=2\widehat{HAE}\Rightarrow \widehat{EFD}=2\widehat{HAE}[/tex]
[tex]\Leftrightarrow \widehat{EFD}=180^{\circ}-\widehat{AKD}\Rightarrow \widehat{EFD}+\widehat{AKD}=180^{\circ}[/tex]
[tex]\Rightarrow EFDKnt\Rightarrow E;F;D;K[/tex] thuộc 1 đường tròn
b) Kẻ đường kính $AP$
Ta có: $OK$ là đường trung bình của [tex]\Delta APC[/tex]
[tex]\Rightarrow PC=2OK[/tex]
Mà: $PC=BH$( $BHCP$ là hình bình hành, Bài toán quen thuộc)
Đến đây cần chứng minh:
[tex]BH\geq DF[/tex]
Gọi $Q$ là trung điểm $BH$
[tex]\Rightarrow QF=QD=QB=QH\Rightarrow BH=QF+QD[/tex]
Mà: [tex]QF+QD\geq FD[/tex]
Dấu ''='' xảy ra khi: $Q$ là trung điểm $FD$
[tex]\Rightarrow BH\geq FD\Rightarrow 2OK\geq FD[/tex]
Dấu ''='' xảy ra khi: $FD=BH$
Mà: $FHDB$ nội tiếp nên $FD;BH$ là đường kính, mà có $2$ góc vuông ($2$ góc....) [tex]\Rightarrow FHDB[/tex] là hình chữ nhật
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
