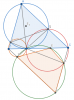
Mấu chốt bài toán là phát hiện ra [TEX]BY//AC,CX//AB[/TEX] thì kéo dài BY cắt CX tại F ta được hình bình hành ABFC.
Ta có: [tex]\widehat{BPD}=\widehat{AQD}=\widehat{PXC}\Rightarrow CX//AB[/tex]
Tương tự thì [TEX]BY//AC[/TEX]
Kéo dài BY cắt CX tại F thì ABFC là hình bình hành.
Vì E,F đối xứng qua trung điểm BC, A,F đối xứng qua trung điểm BC nên [TEX]AD//EF[/TEX]
Ta có: [tex]\widehat{FXD}=\widehat{APD}=\widehat{ADC}=\widehat{FED}\Rightarrow DEXF[/tex] nội tiếp
[tex]\widehat{DXF}=\widehat{APD}=180^o-\widehat{AQD}=180^o-\widehat{DYF} \Rightarrow DYXF[/tex] nội tiếp.
Từ đó D,E,X,Y thuộc cùng 1 đường tròn.
Hình vẽ:
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Em cảm ơn mọi người nhiều ạ.
