5)
a) Chứng minh: [imath]4 \cos x . \cos \left (\dfrac{\pi}{3} + x \right ). \cos \left ( \dfrac{\pi}{3} - x \right ) = \cos 3x[/imath]
b) Áp dụng câu a) chứng minh [imath]\cos 10^o . \cos 20^o . \cos 30^o...\cos 80^o = \dfrac{3}{256}[/imath]
View attachment 204524Chứng minh bài này như thế nào vậyạ?
Gawr Gura
Bạn nên đọc lại công thức 1 chút là làm được liền á kiki
-------------------------------------------------------------------------------------
a) Ta có:
[imath]\cos \left(\dfrac{\pi}{3}+x\right) \cos \left(\dfrac{\pi}{3}-x\right) = \dfrac{1}{2} \cdot \left(\cos (2x)+\cos \left(\dfrac{2\pi}{3} \right)\right) =\dfrac{1}{2} \left (\cos (2x) - \dfrac{1}{2}\right )[/imath]
[imath]\Rightarrow 4 \cos (x) \cos \left (\dfrac{\pi}{3}+x) cos(\dfrac{\pi}{3}-x \right) = 2 \cos (x) \cos (2x) - \cos (x) = \cos (3x) + \cos (x) -\ cos (x) = \cos (3x)[/imath]
b) Công thức được viết lại dưới dạng độ là thay [imath]\dfrac{\pi}{3} = 60^\circ[/imath]
Giờ ghép thoi [imath]\cos 10^\circ \cdot \cos 70^\circ \cdot \cos 50^\circ = \dfrac{\cos 30^\circ}{4} = \dfrac{\sqrt{3}}{8}[/imath]
[imath]\cos 20^\circ \cdot \cos 80^\circ \cdot \cos 40^\circ = \dfrac{\cos 60^\circ}{4}=\dfrac{1}{8}[/imath]
[imath]\cos 30^\circ=\dfrac{\sqrt{3}}{2} ; \cos 60^\circ=\dfrac{1}{2}[/imath]
Từ đó nhân vào ra vế trái = vế phải
-----------------------------------------------------------------------------------
Chúc bạn thành công trong chương Lượng giác nhé, phần này nhiều cái hay lắm đó.
Bạn có thể tham khảo thêm kiến thức ở box Toán nhé
:Tonton4 Helloooo, vì bài viết học thuật dễ bị trôi quá nên chị làm topic này để tổng hợp link cho mấy đứa tiện cho việc ôn tập, ai lớp nào thì vào làm bài vận dụng mà các anh chị soạn để quen dần với cách trình bày nhé, cũng như là một lời cảm ơn vì đã soạn tài liệu cho mấy đứa nè, không cần...
diendan.hocmai.vn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
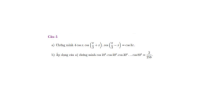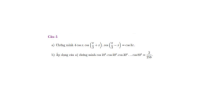Chứng minh bài này như thế nào vậyạ?
