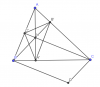
Cho tam giác ABC có 3 góc nhọn, gọi A', B', C', lần lượt là hình chiếu của các đỉnh A,B,C lên các đỉnh đối diện và H là trực tâm của tam giác ABC.
1/ Chứng minh H là tâm đường tròn nội tiếp tam giác A'B'C'
2/ Chứng minh các đường tròn ngoại tiếp các tam giác HAB,HAC,HBC và đường tròn ngoại tiếp tam giác ABC có bán kính bằng nhau
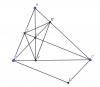
a) Ta có các tứ giác [TEX]BC'HA';C'AB'H;B'CA'H[/TEX] là các tứ giác nội tiếp nên
- [tex]\widehat{C'A'H}=\widehat{C'BH}[/tex]
- [tex]\widehat{HA'B'}=\widehat{HCB'}[/tex]
Mà [tex]\widehat{C'BH}=\widehat{B'CH}[/tex] (cùng phụ với [tex]\widehat{BAC}[/tex])
[tex]\Rightarrow \widehat{C'A'H}=\widehat{B'A'H}[/tex]
[tex]\Rightarrow A'H[/tex] là tia phân giác của [tex]\widehat{C'A'B'}[/tex]
Tương tự: [tex] B'H[/tex] là tia phân giác của [tex]\widehat{C'B'A'}[/tex]
Suy ra $H$ là tâm đường tròn nội tiếp [tex]\Delta A'B'C'(dpcm)[/tex]
b) Từ $B$ kẻ tia [tex]Bx//CH[/tex]
Từ $C$ kẻ tia [tex]Cy//BH[/tex]
$Bx$ cắt $Cy$ tại D
[tex]\Rightarrow BHCD[/tex] là hình bình hành
[tex]\Rightarrow \widehat{BHC}=\widehat{BDC}[/tex]
Ta có tứ giác [TEX]B'CA'H[/TEX] là tứ giác nội tiếp nên
[tex]180^{\circ}=\widehat{C'AB'}+\widehat{C'HB'}=\widehat{BAC}+\widehat{BHC}=\widehat{BAC}+\widehat{BDC}[/tex]
[tex]\Rightarrow ABDC[/tex] là tứ giác nội tiếp
[tex]\Rightarrow \Delta BDC[/tex] nội tiếp đường tròn ngoại tiếp tam giác ABC
Suy ra đường tròn ngoại tiếp [tex]\Delta BDC[/tex] và đường tròn ngoại tiếp [tex]\Delta ABC[/tex] có bán kính bằng nhau
Mà [tex]\Delta BDC=\Delta CHB[/tex]
Nên đường tròn ngoại tiếp các [tex]\Delta HBC[/tex] và đường tròn ngoại tiếp [tex]\Delta ABC[/tex] có bán kính bằng nhau
Tương tự...
Vậy đường tròn ngoại tiếp các tam giác HAB,HAC,HBC và đường tròn ngoại tiếp tam giác ABC có bán kính bằng nhau (đpcm)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
