1/ Cho tam giác ABC có 3 góc nhọn (AB < AC ) đường cao AD và trung tuyến AM . Chứng minh :
a/ BD.DC= (BC^2/4) - MD^2
b/ AM^2 = ( AB^2/2) +( AC^2/2)-(BC^2/2)
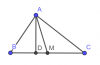
a) Ta có [tex]\widehat{DAM}+\widehat{AMD}=90^{\circ}\Rightarrow \widehat{AMB}<90^{\circ}\Rightarrow \widehat{MAB}+\widehat{ABM}>90^{\circ}[/tex]
[tex]\widehat{BAD}+\widehat{ABD}=90^{\circ};\widehat{BAM}+\widehat{ABD}>90^{\circ}\\\Rightarrow \widehat{BAD}<\widehat{BAM}[/tex]
Suy ra tia $AD$ nằm giữa 2 tia $AB$ và $AM$
Hay điểm $D$ nằm giữa $B$ và $M$
Ta có:
[tex]\frac{BC^2}{4}-MD^2=BM^2-MD^2=(BM-MD)(BM+MD)=BD.(CM+MD)=BD.CD(dpcm)[/tex]
b) Theo định lý $Pythagores$ ta có:
[tex]AB^2+AC^2\\=(BD^2+AD^2)+(CD^2+AD^2)\\=2AD^2+BD^2+CD^2\\=2(AM^2-DM^2)+(BM-DM)^2+(DM+CM)^2\\=2AM^2-2DM^2+BM^2-2.BM.DM+DM^2+DM^2+2DM.CM+CM^2\\=2AM^2+BM^2+CM^2(vì:BM=CM)\\=2AM^2+\frac{BC^2}{4}+\frac{BC^2}{4}\\=2AM^2+\frac{BC^2}{2}\\\Rightarrow AM^2=\frac{AB^2}{2}+\frac{AC^2}{2}-\frac{BC^2}{2}(dpcm)[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
