Nguồn: Đề thi chọn ĐTQG của trường THPT Chuyên KHTN năm 2015, Trần Quang Hùng.
Lời giải sau đây của Moderator Luis González bên AoPs.
Gọi [imath]B_1 \neq X[/imath] là giao điểm thứ [imath]2[/imath] của [imath](AEX)[/imath] và đường tròn đường kính [imath]BD[/imath]. [imath]BB_1[/imath] cắt [imath]EF[/imath] tại [imath]B_2[/imath].
Ta có [imath]\widehat{EB_2B_1}=\widehat{B_1BD}=\widehat{B_1XD}[/imath] nên [imath]EXB_1B_2[/imath] nội tiếp hay [imath]B_2 \in (AEX)[/imath]
Từ đó [imath]\widehat{B_1BD}=\widehat{EB_2B_1}=\widehat{EAB_1}[/imath] nên [imath](ABB_1)[/imath] tiếp xúc với [imath]BC[/imath].
Tương tự với điểm [imath]C_1[/imath] là giao điểm thứ [imath]2[/imath] của [imath](AFY)[/imath] và đường tròn đường kính [imath]CD[/imath] thì [imath](AC_1C)[/imath] tiếp xúc [imath]BC[/imath].
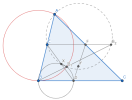
Xét phép nghịch đảo đối xứng [imath]\mathcal{I}[/imath] tâm [imath]A[/imath], phương tích [imath]\overline{AB} \cdot \overline{AC}[/imath], trục [imath]AD[/imath].
[imath]\mathcal{I}: B \leftrightarrow C, BC \leftrightarrow (ABC), (ABB_1) \leftrightarrow (I_1), (ACC_1) \leftrightarrow (I_2)[/imath]
Ta sẽ đi tìm tính chất của [imath](I_1)[/imath].
Gọi [imath]J_1[/imath] là trung điểm của [imath]BD[/imath], [imath]I_1'[/imath] đối xứng với [imath]I_1[/imath] qua [imath]AD[/imath].
Theo tính chất phép nghịch đảo thì [imath]A,J_1,I_1'[/imath] thẳng hàng nên [imath]AJ_1[/imath] và [imath]AI_1[/imath] đẳng giác trong [imath]\widehat{BAC}[/imath]
Gọi [imath]K[/imath] là điểm chính giữa cung nhỏ [imath]BC[/imath] thì [imath]\mathcal{I}: D \leftrightarrow K[/imath] nên [imath](I_1)[/imath] đi qua [imath]C,K[/imath].
Gọi [imath]B_3 \neq D,B_4 \neq K[/imath] lần lượt là giao điểm của [imath](ABB_1)[/imath], [imath](I_1)[/imath] với [imath]AD[/imath].
Khi đó [imath]\mathcal{I}: B_3 \leftrightarrow B_4[/imath] nên [imath]AB_3\cdot AB_4=AD \cdot AK[/imath]
[imath]\Rightarrow \dfrac{AB_3}{AK}=\dfrac{AD}{AB_4}[/imath]
Mặt khác, [imath]A,J_1,I_1'[/imath] thẳng hàng nên [imath]A[/imath] là tâm vị tự ngoài của [imath](J_1)[/imath] và [imath](I_1',I_1'K)[/imath]
[imath]\Rightarrow J_1D \parallel I_1'B_4[/imath]
Mà [imath](I_1)[/imath] đối xứng [imath](I_1')[/imath] qua [imath]AD[/imath] nên [imath]I_1KI_1'B_4[/imath] là hình thoi hay [imath]I_1K \parallel I_1'B_4 \parallel J_1D \equiv BC[/imath]
[imath]\Rightarrow I_1K[/imath] là tiếp tuyến của (O)$
Mà [imath]I_1K=I_1C[/imath] nên [imath]I_1C[/imath] cũng là tiếp tuyến của [imath](O)[/imath]
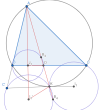
Từ đó [imath]\mathcal{I}: B_1 \leftrightarrow (I_1) \cap I_1C=M[/imath]
Tương tự [imath]\mathcal{I}: C_1 \leftrightarrow (I_2) \cap I_2B = N[/imath]
Với [imath]\mathcal{I}: E \leftrightarrow E',F \leftrightarrow F'[/imath] thì vì [imath]\begin{cases} AE \cdot AE'=AF \cdot AF' \\ E' \in AC \\ F' \in AB \end{cases} \Rightarrow \dfrac{AE'}{AF'}=\dfrac{AF}{AE}=\dfrac{AC}{AB}[/imath] nên [imath]E'F' \parallel BC[/imath]
Ta có: [imath]\mathcal{I}:(AEX) \leftrightarrow E'M, (AFY) \leftrightarrow F'N, P \leftrightarrow E'M \cap F'N[/imath] (ở đây anh lấy [imath](AEX) \cap (AFY) = \lbrace A,P \rbrace[/imath] vì lỡ trùng điểm)
Để chứng minh [imath]P[/imath] thuộc trung tuyến qua đỉnh [imath]A[/imath] của [imath]\Delta ABC[/imath] thì ta sẽ chứng minh [imath]E'M \cap F'N[/imath] nằm trên đường đối trung đi qua [imath]A[/imath] của [imath]\Delta ABC[/imath].
Tới đây ta phát biểu lại bài toán như sau:
"Cho [imath]\Delta ABC[/imath] nội tiếp [imath](O)[/imath] có [imath]E \in AC,F \in AB[/imath] sao cho [imath]EF \parallel BC[/imath]. Gọi [imath]K[/imath] là điểm chính giữa cung nhỏ [imath]BC[/imath], tiếp tuyến tại [imath]K[/imath] của [imath](O)[/imath] cắt tiếp tuyến tại [imath]B,C[/imath] của [imath](O)[/imath] lần lượt tại [imath]I_2,I_1[/imath]. [imath]M[/imath] là giao điểm của [imath](I_1,I_1C)[/imath] và [imath]I_1C[/imath]. [imath]N[/imath] là giao điểm của [imath](I_2,I_2B)[/imath] với [imath]I_2B[/imath]. Chứng minh giao điểm của [imath]EM[/imath] cắt [imath]FN[/imath] tại điểm thuộc đường đối trung đi qua [imath]A[/imath] của [imath]\Delta ABC[/imath]."
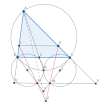
Gọi giao điểm [imath]MN[/imath] với [imath]AB,AC[/imath] lần lượt là [imath]U,V[/imath]; [imath]BN[/imath] cắt [imath]CM[/imath] tại [imath]S[/imath], [imath]EM[/imath] cắt [imath]FN[/imath] tại [imath]P[/imath]. Ta sẽ chứng minh [imath]A,S,P[/imath] thẳng hàng.
Ta thấy [imath]I_1I_2 \parallel BC[/imath] nên [imath]UV \equiv MN \parallel BC[/imath]
Từ đó [imath](AB,FU)=(AC,EY) \Rightarrow N(AB,FU)=M(AC,EY) \Rightarrow N(AS,PM)=M(AS,PN) \Rightarrow A,S,P[/imath] thẳng hàng.
Vậy ta có đpcm.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Đề thi ôn tập chọn HSGQG
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
