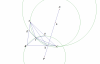
Cho tam giác $ABC$ ngoại tiếp $(I)$. Gọi $X$,$Y$,$Z$ lần lượt là tiếp điểm của đường tròn bàng tiếp góc $A$,$B$,$C$ với $BC$,$CA$,$AB$ . Chứng minh rằng $(AIX)$,$(BIY)$,$(CIZ)$ đồng trục
Hình gửi kèm ạ :
View attachment 194875
@Mộc Nhãn Help me :>
Mọi người giúp em với ạ !!
Cảm ơn mọi người nhiều !!
Bài này mình làm được vì có sự giúp đỡ từ thầy mình nhé :3
________________________________________________
Dễ dàng nhận thấy bài toán trên sẽ tương đương với bài toán sau :
Cho tam giác $ABC$ nội tiếp $(O)$ với ba đường cao $AD,BE,CF$ cắt nhau tại $H$. $X,Y,Z$ lần lượt là hình chiếu của $A,B,C$ trên $EF,DF,DE$. Chứng minh rằng $(DHX),(EHY),(FHZ)$ đồng trục
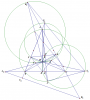
Kẻ các đường kính $HA_1,HB_1,HC_1$ lần lượt của $(DHX),(EHY),(FHZ)$ và đường kính $AN$ của $(O)$
Gọi $A_2,B_2,C_2$ đối xứng với $A_1,B_1,C_1$ qua trung điểm của $BC,CA,AB$
Thì điều cần chứng minh sẽ tương đương chứng minh $A_1,B_1,C_1$ thẳng hàng
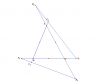
Theo định lí Menelaus thì điều cần chứng minh sẽ tương đương chứng minh $A_2,B_2,C_2$ thẳng hàng
Gọi trung điểm của $BC$ là $P$ , đường tròn Euler của tam giác $ABC$ là $\omega $
Do đó tứ giác $FDPE$ nội tiếp $(\omega )$
Ta có [tex]\overline{D,C,A_1}[/tex] do [tex]\widehat{HDC}=\widehat{HDA_1}=90^{\circ}[/tex]
và [tex]\overline{H,P,N}[/tex] , $P$ là trung điểm của $HN$(tính chất quen thuộc rồi ^^)
và [tex]\overline{A,X,O}[/tex] (cũng quen thuộc luôn :vv)
Ta có [tex]\widehat{XNC}=\widehat{ABC}=\widehat{AEF}[/tex]
do đó $XECN$ nội tiếp
[tex]\Rightarrow AX.AN=AE.AC=AH.AD\Rightarrow N \in (HDX)\\ \Rightarrow \widehat{HNA_1}=\widehat{HDA_1} =90^{\circ}[/tex]
Mặt khác $A_2HA_1N$ là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm)
[tex]\Rightarrow \widehat{A_2HN}=\widehat{HNA_1}=90^{\circ}[/tex]
Xét tam giác $A_2HN$ có $\widehat{A_2HN}=90^{\circ}$ và đường cao $HD$
[tex]\Rightarrow A_2H^2=A_2D.A_2P[/tex]
$\Rightarrow$ $A_2$ thuộc trục đẳng phương của $(\omega )$ và $(H,0)$
Tương tự thì ta cũng được $B_2$ và $C_2$ thuộc trục đẳng phương của $(\omega )$ và $(H,0)$
[tex]\Rightarrow \overline{A_2,B_2,C_2}[/tex] (dpcm)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
