[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Xin chào các bạn ^^
Đây sẽ là topic về chủ đề ôn thi THPTQG có thể giúp cho các bạn trong kì thi sắp tới
1. Con lắc đơn trong điện trường:
PHƯƠNG PHÁP CHUNG:
Khi đặt con lắc vào điện trường đều có véc tơ cường độ điện trường [imath]\overrightarrow{E}[/imath] thì nó chịu tác dụng của trọng lực [imath]\overrightarrow{P}[/imath] và lực điện trường [imath]\overrightarrow{F}=q\overrightarrow{E}[/imath] hợp của hai lực này ký hiệu là:
[imath]\overrightarrow{P'}=\overrightarrow{P}+\overrightarrow{F}(1)[/imath].
P’ được gọi là trọng lực hiệu dụng hay trọng lực biểu kiến.
Chu kì dao động nhỏ của con lắc là: [imath]T'=2\pi \sqrt{\frac{l}{g'}}[/imath]
Do đó để xác định được chu kì T’ ta cần xác định được gia tốc trọng trường hiệu dụng g’. Ta xét một số trường hợp thường gặp:
Trường hợp 1:
[imath]\overrightarrow{E}[/imath] có hướng thẳng đứng xuống dưới
Khi đó thì để xác định chiều của [imath]\overrightarrow{F}[/imath] ta cần biết dấu của [imath]q[/imath].
+) Nếu [imath]q<0[/imath], khi đó [imath]\overrightarrow{F}[/imath] ngược chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng lên trên, từ (1) ta được:
[imath]P'=P-F\Rightarrow mg'=mg-|q|E\Rightarrow g'=g-\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-\frac{|q|E}{m}}}[/imath]
+) Nếu [imath]q>0[/imath], khi đó [imath]\overrightarrow{F}[/imath] cùng chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng xuống dưới, từ (1) ta được:
[imath]P'=P+F\Rightarrow mg'=mg+|q|E\Rightarrow g'=g+\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+\frac{|q|E}{m}}}[/imath]
Trường hợp 2:
[imath]\overrightarrow{E}[/imath] có hướng thẳng đứng lên trên.
+) Nếu [imath]q<0[/imath], khi đó [imath]\overrightarrow{F}[/imath] ngược chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng xuống dưới, từ (1) ta được:
[imath]P'=P+F\Rightarrow mg'=mg+|q|E\Rightarrow g'=g+\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+\frac{|q|E}{m}}}[/imath]
+) Nếu [imath]q>0[/imath], khi đó [imath]\overrightarrow{F}[/imath] cùng chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng lên trên, từ (1) ta được:
[imath]P'=P-F\Rightarrow mg'=mg-|q|E\Rightarrow g'=g-\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-\frac{|q|E}{m}}}[/imath]
Nhận xét:
Tổng hợp cả hai trường hợp và các khả năng trong hai trường hợp trên ta thấy rằng khi véc tơ cường độ điện trường E có phương thẳng đứng (chưa xác định lên trên hay xuống dưới) thì ta luôn có [imath]g'=g\pm \frac{|q|E}{m}[/imath]. Từ đây, dựa vào gia tốc g’ lớn hơn hay nhỏ hơn g và dấu của điện tích q ta có thể xác định được ngay chiều của véc tơ cường độ điện trường.
Trường hợp 3:
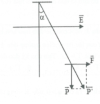
[imath]\overrightarrow{E}[/imath] có phương ngang, khi đó [imath]\overrightarrow{F}[/imath] cũng có phương ngang.
Do trọng lực P hướng xuống nên [imath]\overrightarrow{F}\perp \overrightarrow{P}[/imath]
Từ đó:
[imath]P'^{2}=P^{2}+F^{2}\Rightarrow (mg')^{2}=(mg)^{2}+(|q|E)^{2}[/imath]
[imath]\Rightarrow g'=\sqrt{g^{2}+(\frac{|q|E}{m})^{2}}\Rightarrow T'=2\pi \sqrt{\frac{l}{g'}}[/imath]
Góc lệch của con lắc so với phương ngang ( hay còn gọi là vị trí cân bằng của con lắc trong điện trường ) là [imath]\alpha[/imath] được cho bởi [imath]tan \alpha =\frac{F}{P}=\frac{|q|E}{mg}[/imath]
2. Con lắc đơn trong thang máy:
Con lắc treo trong thang máy chuyển động với gia tốc [imath]\overrightarrow{a_{qt}}[/imath] chịu thêm lực quán tính [imath]\overrightarrow{F_{qt}}=m.\overrightarrow{a_{qt}}[/imath]
+) Thang máy đi lên nhanh dần đều (hoặc xuống chậm dần đều):
[imath]g'=g+a\Rightarrow T=2\pi\sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+a}}[/imath]
+) Thang máy đi lên chậm dần đều (hoặc xuống nhanh dần đều):
[imath]g'=g-a\Rightarrow T=2\pi\sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-a}}[/imath]
3. Con lắc đơn trong toa xe:
Con lắc chịu thêm lực quán tính theo phương ngang:
[imath]\Rightarrow g'=\sqrt{g^{2}+a^{2}}\Rightarrow T=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{\sqrt{g^{2}+a^{2}}}}[/imath]
II. Ví dụ:
VD1:
Một con lắc đơn có chiều dài dây treo [imath]l=50cm[/imath] và vật nhỏ có khối lượng [imath]m = 0,01 (kg)[/imath] mang điện tích [imath]q=5.10^{-6}C[/imath] được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà véc tơ cường độ điện trường có độ lớn [imath]E=10^{4} (V/m)[/imath] và hướng thẳng đứng xuống dưới. Lấy g=10m/s2. Tính chu kỳ dao động điều hòa của con lắc.
VD2:Con lắc đơn dao động với chu kì 2s khi treo trong thang máy đứng yên. Nếu thang máy đi xuống chậm dần đều với gia tốc g/10 thì chu kì dao động của con lắc là bao nhiêu?
Chúc các bạn học tốt


Đây sẽ là topic về chủ đề ôn thi THPTQG có thể giúp cho các bạn trong kì thi sắp tới
CON LẮC ĐƠN VÀ CÁC LỰC LẠ
I. Lý Thuyết 1. Con lắc đơn trong điện trường:
PHƯƠNG PHÁP CHUNG:
Khi đặt con lắc vào điện trường đều có véc tơ cường độ điện trường [imath]\overrightarrow{E}[/imath] thì nó chịu tác dụng của trọng lực [imath]\overrightarrow{P}[/imath] và lực điện trường [imath]\overrightarrow{F}=q\overrightarrow{E}[/imath] hợp của hai lực này ký hiệu là:
[imath]\overrightarrow{P'}=\overrightarrow{P}+\overrightarrow{F}(1)[/imath].
P’ được gọi là trọng lực hiệu dụng hay trọng lực biểu kiến.
Chu kì dao động nhỏ của con lắc là: [imath]T'=2\pi \sqrt{\frac{l}{g'}}[/imath]
Do đó để xác định được chu kì T’ ta cần xác định được gia tốc trọng trường hiệu dụng g’. Ta xét một số trường hợp thường gặp:
Trường hợp 1:
[imath]\overrightarrow{E}[/imath] có hướng thẳng đứng xuống dưới
Khi đó thì để xác định chiều của [imath]\overrightarrow{F}[/imath] ta cần biết dấu của [imath]q[/imath].
+) Nếu [imath]q<0[/imath], khi đó [imath]\overrightarrow{F}[/imath] ngược chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng lên trên, từ (1) ta được:
[imath]P'=P-F\Rightarrow mg'=mg-|q|E\Rightarrow g'=g-\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-\frac{|q|E}{m}}}[/imath]
+) Nếu [imath]q>0[/imath], khi đó [imath]\overrightarrow{F}[/imath] cùng chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng xuống dưới, từ (1) ta được:
[imath]P'=P+F\Rightarrow mg'=mg+|q|E\Rightarrow g'=g+\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+\frac{|q|E}{m}}}[/imath]
Trường hợp 2:
[imath]\overrightarrow{E}[/imath] có hướng thẳng đứng lên trên.
+) Nếu [imath]q<0[/imath], khi đó [imath]\overrightarrow{F}[/imath] ngược chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng xuống dưới, từ (1) ta được:
[imath]P'=P+F\Rightarrow mg'=mg+|q|E\Rightarrow g'=g+\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+\frac{|q|E}{m}}}[/imath]
+) Nếu [imath]q>0[/imath], khi đó [imath]\overrightarrow{F}[/imath] cùng chiều [imath]\overrightarrow{E}[/imath]. Từ đó [imath]\overrightarrow{F}[/imath] hướng thẳng đứng lên trên, từ (1) ta được:
[imath]P'=P-F\Rightarrow mg'=mg-|q|E\Rightarrow g'=g-\frac{|q|E}{m}[/imath]
Chu kỳ dao động của con lắc khi đặt trong điện trường là:
[imath]T'=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-\frac{|q|E}{m}}}[/imath]
Nhận xét:
Tổng hợp cả hai trường hợp và các khả năng trong hai trường hợp trên ta thấy rằng khi véc tơ cường độ điện trường E có phương thẳng đứng (chưa xác định lên trên hay xuống dưới) thì ta luôn có [imath]g'=g\pm \frac{|q|E}{m}[/imath]. Từ đây, dựa vào gia tốc g’ lớn hơn hay nhỏ hơn g và dấu của điện tích q ta có thể xác định được ngay chiều của véc tơ cường độ điện trường.
Trường hợp 3:
[imath]\overrightarrow{E}[/imath] có phương ngang, khi đó [imath]\overrightarrow{F}[/imath] cũng có phương ngang.
Do trọng lực P hướng xuống nên [imath]\overrightarrow{F}\perp \overrightarrow{P}[/imath]
Từ đó:
[imath]P'^{2}=P^{2}+F^{2}\Rightarrow (mg')^{2}=(mg)^{2}+(|q|E)^{2}[/imath]
[imath]\Rightarrow g'=\sqrt{g^{2}+(\frac{|q|E}{m})^{2}}\Rightarrow T'=2\pi \sqrt{\frac{l}{g'}}[/imath]
Góc lệch của con lắc so với phương ngang ( hay còn gọi là vị trí cân bằng của con lắc trong điện trường ) là [imath]\alpha[/imath] được cho bởi [imath]tan \alpha =\frac{F}{P}=\frac{|q|E}{mg}[/imath]
2. Con lắc đơn trong thang máy:
Con lắc treo trong thang máy chuyển động với gia tốc [imath]\overrightarrow{a_{qt}}[/imath] chịu thêm lực quán tính [imath]\overrightarrow{F_{qt}}=m.\overrightarrow{a_{qt}}[/imath]
+) Thang máy đi lên nhanh dần đều (hoặc xuống chậm dần đều):
[imath]g'=g+a\Rightarrow T=2\pi\sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+a}}[/imath]
+) Thang máy đi lên chậm dần đều (hoặc xuống nhanh dần đều):
[imath]g'=g-a\Rightarrow T=2\pi\sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g-a}}[/imath]
3. Con lắc đơn trong toa xe:
Con lắc chịu thêm lực quán tính theo phương ngang:
[imath]\Rightarrow g'=\sqrt{g^{2}+a^{2}}\Rightarrow T=2\pi \sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{\sqrt{g^{2}+a^{2}}}}[/imath]
II. Ví dụ:
VD1:
Một con lắc đơn có chiều dài dây treo [imath]l=50cm[/imath] và vật nhỏ có khối lượng [imath]m = 0,01 (kg)[/imath] mang điện tích [imath]q=5.10^{-6}C[/imath] được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà véc tơ cường độ điện trường có độ lớn [imath]E=10^{4} (V/m)[/imath] và hướng thẳng đứng xuống dưới. Lấy g=10m/s2. Tính chu kỳ dao động điều hòa của con lắc.
Do [imath]\overrightarrow{E}[/imath] hướng xuống, q>0 nên [imath]\overrightarrow{F}[/imath] hướng xuống [imath]\Rightarrow P'=P+F\Rightarrow mg'=mg+|q|E\Rightarrow g'=g+\frac{|q|E}{m}=15(m/s^{2})[/imath]
Chu kì dao động của con lắc: [imath]T'=2\pi \sqrt{\frac{l}{g'}}=1,15[/imath]
Chu kì dao động của con lắc: [imath]T'=2\pi \sqrt{\frac{l}{g'}}=1,15[/imath]
VD2:Con lắc đơn dao động với chu kì 2s khi treo trong thang máy đứng yên. Nếu thang máy đi xuống chậm dần đều với gia tốc g/10 thì chu kì dao động của con lắc là bao nhiêu?
Thang máy đi xuống chậm dần đều: [imath]T=2\pi\sqrt{\frac{l}{g'}}=2\pi \sqrt{\frac{l}{g+a}}=2\pi \sqrt{\frac{l}{\frac{11}{10}g}}=\sqrt{\frac{10}{11}}.2\pi \sqrt{\frac{l}{g}}=\sqrt{\frac{10}{11}}.2=1,90s[/imath]
Chúc các bạn học tốt


Attachments
Last edited: