[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
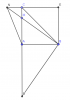
Cho [tex]\Delta ABC[/tex] vuông cân ở A. Gọi M là một điểm thuộc cạnh AC, BM kéo dài cắt đường vuông góc với AC tại C ở N.
a) Chứng minh: [tex]\frac{1}{BM^{2}}+\frac{1}{BN^{2}}=\frac{1}{AC^{2}}[/tex]
b) Cho AC=6cm, BN=10cm. Tính diện tích tứ giác ABCN.
a) Chứng minh: [tex]\frac{1}{BM^{2}}+\frac{1}{BN^{2}}=\frac{1}{AC^{2}}[/tex]
b) Cho AC=6cm, BN=10cm. Tính diện tích tứ giác ABCN.