[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
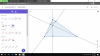
Cho [tex]\Delta ABC[/tex] có các góc đều nhọn, BC = a, H là trực tâm, tia BH, CH lần lượt cắt AC, AB tại M và N.
a. Cho biết [tex]\widehat{NHM}=120^{\circ}[/tex]. Tính MN, AH theo a.
b. CMR: [tex]sin\widehat{ABC}.sin\widehat{ACB}-cos\widehat{ABC}.cos\widehat{ACB}=cos\widehat{BAC}[/tex]
c. Bỏ giả thiết [tex]\widehat{MHN}=120^{\circ}[/tex]. Cho biết [tex]\widehat{BAC}=2\widehat{ABC}[/tex], khi đó cm: [tex]AC^{2}+AB.AC=a^{2}[/tex]
a. Cho biết [tex]\widehat{NHM}=120^{\circ}[/tex]. Tính MN, AH theo a.
b. CMR: [tex]sin\widehat{ABC}.sin\widehat{ACB}-cos\widehat{ABC}.cos\widehat{ACB}=cos\widehat{BAC}[/tex]
c. Bỏ giả thiết [tex]\widehat{MHN}=120^{\circ}[/tex]. Cho biết [tex]\widehat{BAC}=2\widehat{ABC}[/tex], khi đó cm: [tex]AC^{2}+AB.AC=a^{2}[/tex]
Last edited: