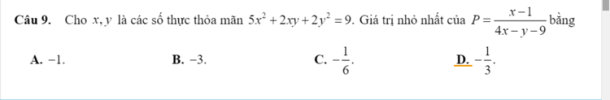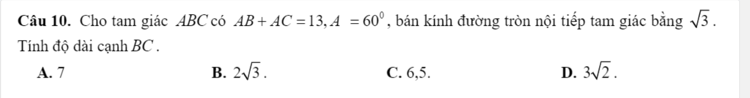Toán 10 Cho tam giác [imath]ABC[/imath] có: [imath]AB + AC = 13; \widehat{A} = 60^o[/imath]

[Lục Lạc]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Câu 9: Cho [imath]x;y[/imath] là các số thực thoả mãn [imath]5x^2 + 2xy + 2y^2 = 9[/imath]. Gía trị nhỏ nhất của [imath]P = \dfrac{x -1}{4x - y - 9}[/imath]


Câu 10: Cho tam giác [imath]ABC[/imath] có: [imath]AB + AC = 13; \widehat{A} = 60^o[/imath], bán kính đường tròn nội tiếp tam giác bằng[imath]\sqrt{3}[/imath]. Tính độ dài cạnh [imath]BC[/imath]
[imath]A. 7[/imath]
[imath]B. 2\sqrt{3}[/imath]
[imath]C.6,5[/imath]
[imath]D. 3\sqrt{2}[/imath]
Giúp em với ạ em cảm ơn

 

[7 1 2 5]

9. Ta có [imath]x-1=P(4x-y-9) \Rightarrow Py=(4P-1)x+1-9P[/imath]
Nếu [imath]P=0 \Rightarrow x=1 \Rightarrow 2y^2+2y-4=0 \Rightarrow 2(y-1)(y+2)=0 \Rightarrow y=1 \vee y=-2[/imath]
Nếu [imath]P \neq 0 \Rightarrow y=\dfrac{4P-1}{P}x+\dfrac{1-9P}{P}[/imath]
Thay vào biểu thức ban đầu ta có [imath]5x^2+2x(\dfrac{4P-1}{P}x+\dfrac{1-9P}{P})+2(\dfrac{4P-1}{P}x+\dfrac{1-9P}{P})^2=9[/imath]
Đặt [imath]t=\dfrac{4P-1}{P} \Rightarrow \dfrac{1-9P}{P}=-(t+5)[/imath]
Khi đó [imath]5x^2+2x(tx-t-5)+2(tx-t-5)^2=9 \Rightarrow (5+2t+2t^2)x^2-(4t^2+20t+2t+10)x+2(t+5)^2=9[/imath]
[imath]\Rightarrow (2t^2+2t+5)x^2-(4t^2+22t+10)x+2t^2+20t+41=0[/imath]
Để tồn tại [imath]x[/imath] thì [imath]\Delta '=(2t^2+11t+5)^2-(2t^2+2t+5)(2t^2+20t+41)=9(t+2)(t-10) \geq 0[/imath]
[imath]\Leftrightarrow t \geq 10 \vee t \leq -2[/imath]
[imath]\Rightarrow \dfrac{4P-1}{P} \geq 10 \vee \dfrac{4P-1}{P} \leq -2[/imath]
[imath]\Rightarrow \dfrac{1}{P} \leq -6 \vee \dfrac{1}{P} \geq 6[/imath]
[imath]\Rightarrow 0 \geq P \geq -\dfrac{1}{6} \vee 0 \leq P \leq \dfrac{1}{6}[/imath]
Từ đó ta thấy [imath]\min P=\dfrac{-1}{6}[/imath]. Dấu [imath]"="[/imath] xảy ra khi [imath]x=\dfrac{7}{5},y=-1[/imath]
10. Kí hiệu [imath]BC=a,CA=b,AB=c[/imath].
Gọi [imath]I[/imath] là tâm đường tròn nội tiếp của [imath]\Delta ABC[/imath], vẽ [imath]ID,ID'[/imath] lần lượt vuông góc với [imath]AB,AC[/imath]
Ta thấy [imath]AD=AD'=\dfrac{b+c-a}{2},ID=ID'=\sqrt{3}[/imath]
Mặt khác [imath]\widehat{IAD}=30^o \Rightarrow AD=\cot \widehat{IAD} \cdot ID=3[/imath]
[imath]\Rightarrow a=b+c-2AD=13-6=7[/imath]

Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Tổng hợp kiến thức cơ bản Hình học 10