View attachment 194973
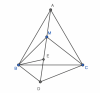
a) CM: $\triangle CMA = \triangle CBD$
Ta có $\widehat{ACM}+\widehat{MCB}=\widehat{MCB}+\widehat{BCD}$
$\implies \widehat{ACM}=\widehat{BCD}$
Xét $\triangle CMA$ và $\triangle CBD$ có
$CM=CD$
$CA=CB$
$\widehat{ACM}=\widehat{BCD}$
Suy ra: $\triangle CAM = \triangle CBD \quad (c-g-c)$
b) CM: $\triangle MBD$ là tam giác vuông.
Vì $MB$ là độ dài cạnh hình vuông diện tích là 3 nên ta có $BM^2=3 \implies BM=\sqrt3$
Lại có $BD=AM=1$ và $MD=MC=2$ (vì $\Delta CAM = \Delta CBD$)
Xét tam giác $BDM$ có:
$BM^2+BD^2=MD^2$
Suy ra $\triangle BDM$ vuông tại $B$
c) Tính $\widehat{BMC}, \widehat{AMB}$ suy ra $A, M, D$ thẳng hàng.
Gọi $E$ là trung điểm $MD$ khi đó $BE=ME=ED=\dfrac{1}2 MD=1 (cm)$ (Vì đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Mà $BD=1 cm$
$\implies \triangle BED$ đều
$\implies \widehat{BID} =60^\circ $
Mà $\triangle BMD$ vuông tại $B$
$\implies \widehat{BMD}=30^\circ$
Lại có $\widehat{BMC}=\widehat{BMD}=\widehat{DMC} = 30^\circ +60^\circ=90^\circ$
Ta có: $\widehat{AMC}=\widehat{BDC}$
Mà $\widehat{BDC}=\widehat{BDE}+\widehat{MDC}=60^\circ + 60^\circ =120^\circ$
Suy ra $\widehat{AMC}=120^\circ$
$\widehat{AMD}=\widehat{AMC}+\widehat{DMC}=120^\circ+ 60^\circ=180^\circ$
Vậy $A,M,D $ thẳng hàng
d) Tính diện tích hình vuông cạnh BC.
Có $\triangle BMD$ vuông tại $B$ ta có
$\sin \widehat{BMD}=\dfrac{BD}{MD}=\dfrac{1}2$
$\widehat{BMD}=30^\circ$
Mà $\triangle CMD$ đều $\implies \widehat{CMD}=60^\circ$
$\implies \widehat{BMC}=\widehat{BMD}+\widehat{CMD}=90^\circ$
Hay $\triangle BMC$ vuông tại $M$
Áp dụng định lý Pytago tính được $BC$ rồi tính diện tích hình vuông nha em
Ngoài ra, em tham khảo thêm kiến thức khác tại topic này nha
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
Và ôn thi học kì cùng box Toán nhé
https://diendan.hocmai.vn/threads/tong-hop-topic-on-thi-hoc-ki.841342/
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
