Toán 9 cho tam giác abc vuông tại a

[fjajifjiejfjhaei]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

giúp em với ạ

 

[iceghost]

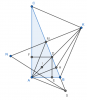
1) Ta có $\widehat{SAB} = 90^\circ - \widehat{MAB} = 90^\circ - \widehat{MBA} = \widehat{SCA}$ nên $\triangle{SAB} \sim \triangle{SCA}$, suy ra $SB \cdot SC = SA^2 = SH \cdot SM$ (theo hệ thức lượng)


2) Ta cần chứng minh $H$ là trực tâm $\triangle{SKN}$

Có một cách chứng minh trực tâm dùng cạnh, đó là: chứng minh $MK \cdot MN = MH \cdot MS$ (sau đó xài tam giác đồng dạng để ra các góc vuông góc nhau).

Điều này tương đương $MK^2 = MA^2$, điều này đúng do $A, K$ thuộc đường tròn tâm $M$ đường kính $BC$.


3) Do $KB = KC$ nên $AD$ là đường phân giác tại đỉnh $A$.

Để chứng minh đẳng thức đpcm, bạn sử dụng $\dfrac{DB}{CB} = \dfrac{DE}{AC}$ và tương tự nhé. Sau đó thay vào, sử dụng định lý Pytago và $DE = DF = AD / \sqrt{2}$ để rút gọn là được.

Để chứng minh $S, E, F$ thẳng hàng, để ý $AEDF$ là hình vuông nên $EF$ vuông góc $AD$ tại trung điểm $I$. Ta chứng minh $SI \perp AD$ bằng tính chất tam giác cân.

Do $\widehat{SAD} = \widehat{SAB} + \widehat{BAD} = \widehat{SCA} + \widehat{CAD} = \widehat{SDA}$ nên tam giác $\triangle{SDA}$ cân tại $S$, ta có đpcm.


Nếu có thắc mắc gì, bạn có thể hỏi lại bên dưới nha. Chúc bạn học tốt!