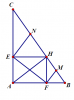
Cho tam giác ABC vuông tại A có AB = 6cm , AC = 8cm. Kẻ AH vuông góc với BC
a) Tính AH
b) Kẻ HE vuông góc với AB ; HF vuông góc với AC. Tính EF
c) Gọi M , N là trung điểm HB , HC. Tứ giác MNEF là hình gì? Tính diện tích tứ giác MNEF
_________________________________________________
a) Áp dụng $Pytago$ vào tam giác vuông $ABC$
[tex]\Rightarrow BC=10[/tex]
Dễ dàng chứng minh được: [tex]\Delta AHB\sim \Delta CAB \Rightarrow \frac{AH}{AB}=\frac{AC}{BC}\Rightarrow AH=\frac{AC.AB}{BC}=\frac{6.8}{10}=4,8[/tex]
b) Dễ dàng có được: $AEHF$ là hình chữ nhật
[tex]\Rightarrow AH=EF=6,8[/tex]
c) Dễ dàng chứng minh được: [tex]AC^2=HC.BC (\Delta AHC\sim \Delta BAC)[/tex]
[tex]\Rightarrow HC=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\Rightarrow HB=10-6,4=3,6[/tex]
* Dễ dàng chứng minh đuợc: [tex]\Delta ENH[/tex] cân [tex]\Rightarrow \widehat{NEH}=\widehat{NHE}[/tex]
Mà: [tex]\widehat{FEH}=\widehat{AHE}[/tex]
Cộng theo vế ta được: [tex]\widehat{NEF}=90^{\circ}[/tex]
CMTT: [tex]\widehat{EFM}=90^{\circ}\Rightarrow EN\parallel FM\Rightarrow ENMF[/tex] là hình thang
Mà: [tex]\widehat{EFM}=90^{\circ}\Rightarrow ENMF[/tex] là hình thang vuông
*[tex]S_{MNEF}=\frac{(EN+MF)EF}{2}[/tex]
Có [tex]HB;HC\Rightarrow HM;HN\Rightarrow MF;NE[/tex]
Khi đó thày vào tính $S$ nhé!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
