Toán 7 Cho tam giác ABC vuông A có B=30°. Cm AC=1/2 BC

[Nguyễn Hữu Nam 2005]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho tam giác ABC vuông A có B=30°. Cm AC=1/2 BC

 

[hdiemht]

Cho tam giác ABC vuông A có B=30°. Cm AC=1/2 BC

_________________
Trên tia đối của tia $AC$ lấy $D$ sao cho $AC=AD$
Từ đó dễ dàng CM được: [tex]\Delta BAC=\Delta BAD\Rightarrow \widehat{ABC}=\widehat{ABD}=30^{\circ}\Rightarrow \widehat{DBC}=60^{\circ}; BD=BC\Rightarrow \Delta BCD[/tex] đều
Mà: [tex]BA[/tex] là đường cao nên cũng là đường trung tuyến suy ra: $AD=AC$ [tex]\Rightarrow AC=\frac{1}{2}DC=\frac{1}{2}BC[/tex]
$P/S:$ Bài này được áp dụng rất nhiều và không cần chứng minh!

 

[Dương Sảng]

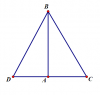
Kẻ từ A một tia cắt BC tại trung điểm O và AO = OD
=> BO = OC
Xét tg BOA và tg COD bằng nhau theo trường hợp c.g.c
=> AB = CD ( hai cạnh tương ứng )
và [tex]\widehat{ABO}=\widehat{DCO}[/tex] ( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong => AB // CD
=> [tex]\widehat{BAC}=\widehat{ACD}=180^{o}[/tex] ( trong cùng phía )
=> [tex]90^{o}+\widehat{ADC}=180^{o} \Rightarrow \widehat{ADC}=90^{o}[/tex]
=> Tam giác ADC vuông tại D
Xét hai tg vuông ABC và ADC bằng nhau theo trường hợp ch-cgv
=> BC = DA ( hai cạnh tương ứng )
mà OC = 1/2 BC ( O là trung điểm )
=> OC = OA
=> Tg OAC cân tại O (1)
Áp dụng tính chất tg vuông ta có :
[tex]\widehat{B}+\widehat{BCA}=90^{o}\Rightarrow \widehat{BCA}=60^{o}[/tex]
hay [tex]\widehat{OCA}=60^{o}[/tex] (2)
Từ (1) và (2) suy ra tg OCA đều.
=> AC = OC
mà OC = 1/2 BC => AC = 1/2 BC ( đpcm )