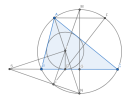
Gọi [imath]D[/imath] là hình chiếu của [imath]I[/imath] trên [imath]BC[/imath], [imath]E[/imath] là giao điểm của [imath]MI[/imath] với [imath](O)[/imath], [imath]N[/imath] là điểm chính giữa cung nhỏ [imath]BC[/imath], [imath]MN,NE[/imath] cắt [imath]BC[/imath] tại [imath]G,S[/imath].
Ta có: [imath]\widehat{MEN}=\widehat{SGN}=90^o \Rightarrow NE.NS=NG.NM[/imath]
Mà [imath]NG.NM=NB^2 \Rightarrow NE.NS=NB^2[/imath]
Mặt khác ta có [imath]NI=NB=NC \Rightarrow NI^2=NE.NS[/imath]
[imath]\Rightarrow \widehat{SIN}=90^o[/imath]
Lại có: [imath]\widehat{IDS}=\widehat{IES}=90^o \Rightarrow IDES[/imath] nội tiếp
[imath]\Rightarrow \widehat{IED}=\widehat{ISD}=\widehat{DIN}=\widehat{INM}=\widehat{IEA}[/imath]
Mà [imath]\widehat{IEB}=\widehat{IEC}[/imath](do [imath]EI[/imath] đi qua điểm chính giữa cung [imath]BC[/imath])
[imath]\Rightarrow \widehat{BED}=\widehat{AEC}[/imath]
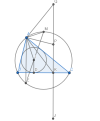
Từ đó ta chứng minh được [imath]\Delta BED \sim \Delta AEC \Rightarrow \dfrac{BE}{BD}=\dfrac{AE}{AC}[/imath]
Mặt khác, [imath]BD=KC=\dfrac{AB+BC-AC}{2}[/imath] nên [imath]\dfrac{BE}{KC}=\dfrac{AE}{AC}[/imath]
Vì [imath]\widehat{AEB}=\widehat{ACK} \Rightarrow \Delta AEB \sim \Delta ACK[/imath]
[imath]\Rightarrow \widehat{ABE}=\widehat{AKC} \Rightarrow \widehat{AMI}=\widehat{AKB}[/imath]
Mà [imath]ABKP[/imath] nội tiếp nên [imath]\widehat{AKB}=\widehat{APB}[/imath]
Tới đây thì ta thấy [imath]\Delta ABC \sim \Delta APQ, \Delta ABP \sim \Delta ACQ \sim \Delta AIM[/imath] nên dễ chứng minh được [imath]M[/imath] là tâm nội tiếp của [imath]APQ[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Ôn tập toán các dạng bài hình học 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
