- 24 Tháng mười hai 2018
- 8
- 1
- 1
- 18
- Ninh Bình
- Trường Trung học Cơ Sở Lê Lợi
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
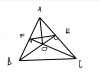
Cho tam giác ABC. Kẻ BE vuông góc với AC, CF vuông góc với AB. Biết BE = CF = 8cm, độ dài các đoạn BF và BC tỉ lệ với 3 và 5.
a) Cm tam giác ABC là tam giác cân.
b) Tính độ dài của BC.
c) BE và CF cắt nhau tại O. Nối A với O, E với F. Cm AO là đường trung trực củađoạn thẳng EF.
a) Cm tam giác ABC là tam giác cân.
b) Tính độ dài của BC.
c) BE và CF cắt nhau tại O. Nối A với O, E với F. Cm AO là đường trung trực củađoạn thẳng EF.