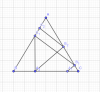
Cho tam giác ABC đều cạnh a. Trên BC lấy điểm A1 sao cho CA1 = x. Gọi B1 là hình chiếu của A1 lên CA, C1 là hình chiếu của B1 lên AB, A2 là hình chiếu của C1 lên BC, B2 là hình chiếu của A2 lên CA,... và cứ liên tục như thế. Tìm x theo a sao cho A2018 trùng A1
mong mọi người trả lời bài viết
$A_1C=x\Rightarrow CB_1=\dfrac{x}{2}$
$\Rightarrow AB_1=a-\dfrac{x}{2}\Rightarrow AC_1=\dfrac{a}{2}-\dfrac{x}{4}$
$\Rightarrow BC_1=\dfrac{a}{2}+\dfrac{x}{4}\Rightarrow BD=\dfrac{a}{4}+\dfrac{x}{8}$
Suy ra $A_2C=a-\dfrac{a}{4}-\dfrac{x}{8}=\dfrac{3a}{4}-\dfrac{x}{8}$
$A_3C=\dfrac{3a}{4}-\dfrac{1}{8}.\left(\dfrac{3a}{4}-\dfrac{x}{8}\right)$
Vậy ta có dãy số để tìm $A_nC$ là
$u_1=x$
$u_n=\dfrac{3a}{4}-\dfrac{u_{n-1}}{8}$
$u_n-\dfrac{2a}{3}=-\dfrac{1}{8}.\left(u_{n-1}-\dfrac{2a}{3}\right)$
$u_n-\dfrac{2a}{3}=\left(-\dfrac18\right)^{n-1}\left(x-\dfrac{2a}{3}\right)$
$A_{2018}C=u_{2018}=\left(-\dfrac18\right)^{2017}\left(x-\dfrac{2a}{3}\right)+\dfrac{2a}{3}=x$ (do $A_1C=x$)
$\Rightarrow x=\dfrac{2a}{3}$
Có gì khúc mắc bạn hỏi lại nhé <3
Ngoài ra em tham khảo thêm kiến thức tại đây nhé
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


